题目内容
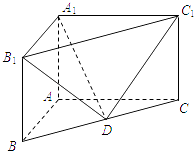
【题目】如图,已知斜三棱柱![]() ,
, ![]() ,
, ![]() ,
, ![]() 在底面
在底面![]() 上的射影恰为
上的射影恰为![]() 的中点
的中点![]() ,且
,且![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求![]() 到平面
到平面![]() 的距离;
的距离;
(3)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)见解析(2)![]() (3)
(3)![]()
【解析】试题分析:(1)由题意得A1D⊥平面ABC,根据面面垂直判定定理得平面A1ACC1⊥平面ABC,由BC⊥AC,根据面面垂直性质定理得BC⊥平面A1ACC1,即得BC⊥AC1,又已知![]() ,所以由线面垂直判定定理得
,所以由线面垂直判定定理得![]() 平面
平面![]() ;(2)利用向量求线面距离,首先求平面法向量,再根据向量投影求距离:先根据条件建立空间直角坐标系,设立各点坐标,利用方程组求平面法向量;再根据向量投影求距离(3)利用向量求二面角:先根据条件建立空间直角坐标系,设立各点坐标,利用方程组求平面法向量;再根据向量数量积求法向量夹角,最后根据二面角与法向量夹角关系求二面角
;(2)利用向量求线面距离,首先求平面法向量,再根据向量投影求距离:先根据条件建立空间直角坐标系,设立各点坐标,利用方程组求平面法向量;再根据向量投影求距离(3)利用向量求二面角:先根据条件建立空间直角坐标系,设立各点坐标,利用方程组求平面法向量;再根据向量数量积求法向量夹角,最后根据二面角与法向量夹角关系求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
试题解析:解:(1)∵A1在底面ABC上的射影为AC的中点D,
∴平面A1ACC1⊥平面ABC,
∵BC⊥AC且平面A1ACC1∩平面ABC=AC,
∴BC⊥平面A1ACC1,
∴BC⊥AC1,
∵AC1⊥BA1且BC∩BA1=B,
∴AC1⊥平面A1BC。
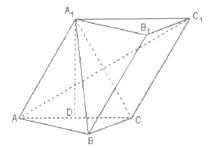
(2)如图所示,以C为坐标原点建立空间直角坐标系,
∵AC1⊥平面A1BC,
∴AC1⊥A1C,
∴四边形A1ACC1是菱形,
∵D是AC的中点,
∴∠A1AD=60°,
∴A(2,0,0),A1(1,0,![]() ),B(0,2,0), C1(-1,0,
),B(0,2,0), C1(-1,0,![]() ),
),
∴![]() =(1,0,
=(1,0,![]() ),
),![]() =(-2,2,0),
=(-2,2,0),
设平面A1AB的法向量![]() =(x,y,z),
=(x,y,z),
∴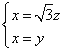 ,
,
令z=1,
∴![]() =(
=(![]() ,
,![]() ,1),
,1),
∵![]() =(2,0,0),
=(2,0,0),
∴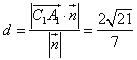 ,
,
∴C1到平面A1AB的距离是![]()
(3)平面A1AB的法向量![]() =(
=(![]() ,
,![]() ,1),平面A1BC的法向量
,1),平面A1BC的法向量![]() =(-3,0,
=(-3,0,![]() ),
),
∴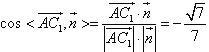 ,
,
设二面角A-A1B-C的平面角为θ,θ为锐角,
∴![]() ,
,
∴二面角A-A1B-C的余弦值为![]()

 全能练考卷系列答案
全能练考卷系列答案【题目】某城市理论预测2007年到2011年人口总数与年份的关系如表所示
年份2007+x(年) | 0 | 1 | 2 | 3 | 4 |
人口数y(十万) | 5 | 7 | 8 | 11 | 19 |
(1)请根据表提供的数据,求最小二乘法求出y关于x的线性回归方程;
(2)据此估计2012年该城市人口总数.
参考公式: 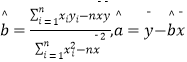 .
.