Question

【题目】已知a+b+c=2，且a、b、c是正数，求证： + + ≥ ．

Answer 1

【答案】证明：a+b+c=2，且a、b、c是正数，
可得1= （2a+2b+2c），
+ + =（ + + ）×1
= （2a+2b+2c）（ + + ）
= [（a+b）+（b+c）+（c+a）]（ + + ）
≥ 3 3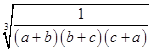
= （当且仅当a=b=c取得等号）．
则 + + ≥
【解析】由条件可得1= （2a+2b+2c），则 + + = （2a+2b+2c）（ + + ）= [（a+b）+（b+c）+（c+a）]（ + + ），再由三元基本不等式，以及不等式的可乘性，即可得证．
【考点精析】根据题目的已知条件，利用不等式的证明的相关知识可以得到问题的答案，需要掌握不等式证明的几种常用方法:常用方法有：比较法（作差，作商法）、综合法、分析法；其它方法有：换元法、反证法、放缩法、构造法，函数单调性法，数学归纳法等．