题目内容
已知向量m=(sin x,1),n= ,函数f(x)=(m+n)·m.
,函数f(x)=(m+n)·m.
(1)求函数f(x)的最小正周期T及单调递增区间;
(2)已知a,b,c分别为△ABC内角A,B,C的对边,A为锐角,a=2 ,c=4,且f(A)是函数f(x)在
,c=4,且f(A)是函数f(x)在 上的最大值,求△ABC的面积S.
上的最大值,求△ABC的面积S.
 ,函数f(x)=(m+n)·m.
,函数f(x)=(m+n)·m.(1)求函数f(x)的最小正周期T及单调递增区间;
(2)已知a,b,c分别为△ABC内角A,B,C的对边,A为锐角,a=2
 ,c=4,且f(A)是函数f(x)在
,c=4,且f(A)是函数f(x)在 上的最大值,求△ABC的面积S.
上的最大值,求△ABC的面积S.(1)π 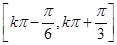 (k∈Z).
(k∈Z).
(2)2
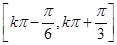 (k∈Z).
(k∈Z).(2)2

(1)f(x)=(m+n)·m=sin2x+1+ sin xcos x+
sin xcos x+ =
= +1+
+1+ sin 2x+
sin 2x+ =
= sin 2x-
sin 2x- cos 2x+2=sin
cos 2x+2=sin +2.
+2.
因为ω=2,所以T= =π.
=π.
由2kπ-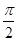 ≤2x-
≤2x-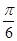 ≤2kπ+
≤2kπ+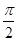 (k∈Z)
(k∈Z)
得kπ-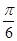 ≤x≤kπ+
≤x≤kπ+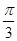 (k∈Z),
(k∈Z),
故所求单调递增区间为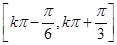 (k∈Z).
(k∈Z).
(2)由(1)知,f(A)=sin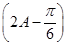 +2,
+2,
又A∈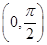 ,∴-
,∴-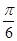 <2A-
<2A-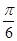 <
< .
.
由正弦函数图象可知,当2A-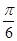 =
=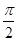 ,
,
即A=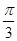 时,f(x)取得最大值3,
时,f(x)取得最大值3,
由余弦定理,a2=b2+c2-2bccos A.
可得12=b2+16-2×4b× ,∴b=2.
,∴b=2.
从而S= bcsin A=
bcsin A= ×2×4×sin
×2×4×sin 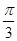 =2
=2 .
.
 sin xcos x+
sin xcos x+ =
= +1+
+1+ sin 2x+
sin 2x+ =
= sin 2x-
sin 2x- cos 2x+2=sin
cos 2x+2=sin +2.
+2.因为ω=2,所以T=
 =π.
=π.由2kπ-
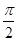 ≤2x-
≤2x-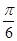 ≤2kπ+
≤2kπ+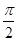 (k∈Z)
(k∈Z)得kπ-
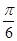 ≤x≤kπ+
≤x≤kπ+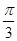 (k∈Z),
(k∈Z),故所求单调递增区间为
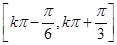 (k∈Z).
(k∈Z).(2)由(1)知,f(A)=sin
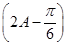 +2,
+2,又A∈
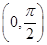 ,∴-
,∴-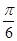 <2A-
<2A-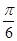 <
< .
.由正弦函数图象可知,当2A-
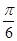 =
=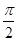 ,
,即A=
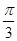 时,f(x)取得最大值3,
时,f(x)取得最大值3,由余弦定理,a2=b2+c2-2bccos A.
可得12=b2+16-2×4b×
 ,∴b=2.
,∴b=2.从而S=
 bcsin A=
bcsin A= ×2×4×sin
×2×4×sin 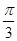 =2
=2 .
.
练习册系列答案
相关题目
 :函数
:函数 是最小正周期为
是最小正周期为 的周期函数,命题
的周期函数,命题 :函数
:函数 在
在 上单调递减,则下列命题为真命题的是( )
上单调递减,则下列命题为真命题的是( )

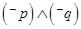

 的值为____________.
的值为____________.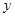 轴上的角的集合是
轴上的角的集合是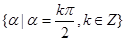 ;
;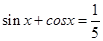 ,则
,则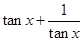 的值为
的值为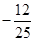 ;
;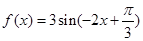 在区间
在区间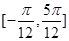 内是减函数;
内是减函数;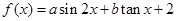 ,且
,且 ,则
,则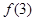 的值为
的值为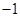 ;
;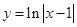 的图像与函数
的图像与函数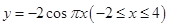 的图像所有交点的横坐标之和等于6.
的图像所有交点的横坐标之和等于6. +
+ sin ωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
sin ωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
 ,且x0∈
,且x0∈ ,求f(x0+1)的值.
,求f(x0+1)的值.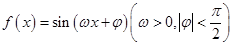 的部分图象如图所示.
的部分图象如图所示.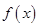 的解析式,并写出
的解析式,并写出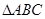 的内角分别是A,B,C,角A为锐角,且
的内角分别是A,B,C,角A为锐角,且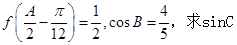 的值.
的值.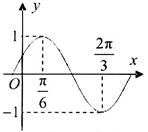
 x+
x+ )(
)( >0,|
>0,| |<
|<  ,x∈R)的部分图象如图,则函数表达式为
,x∈R)的部分图象如图,则函数表达式为 
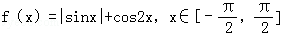 ,则函数f(x)的最小值是( )
,则函数f(x)的最小值是( )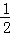
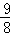
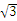 sin2x的最小正周期T为_______.
sin2x的最小正周期T为_______.