题目内容
函数f(x)=6cos2 +
+ sin ωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
sin ωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.

(1)求ω的值及函数f(x)的值域;
(2)若f(x0)= ,且x0∈
,且x0∈ ,求f(x0+1)的值.
,求f(x0+1)的值.
 +
+ sin ωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
sin ωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
(1)求ω的值及函数f(x)的值域;
(2)若f(x0)=
 ,且x0∈
,且x0∈ ,求f(x0+1)的值.
,求f(x0+1)的值.(1)ω=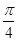 , [-2
, [-2 ,2
,2 ]
]
(2)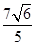
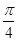 , [-2
, [-2 ,2
,2 ]
](2)
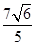
(1)由已知可得,
f(x)=3cos ωx+ sin ωx=2
sin ωx=2 sin
sin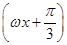 ,
,
又正三角形ABC的高为2 ,从而BC=4,
,从而BC=4,
所以函数f(x)的周期T=4×2=8,即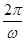 =8,ω=
=8,ω=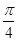 .
.
函数f(x)的值域为[-2 ,2
,2 ].
].
(2)因为f(x0)= ,由(1)有
,由(1)有
f(x0)=2 sin
sin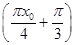 =
= ,
,
即sin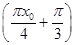 =
=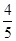
由x0∈ ,知
,知 ∈
∈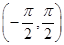 ,
,
所以cos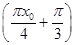 =
= 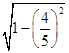 =
=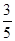 .
.
故f(x0+1)=2 sin
sin
=2 sin
sin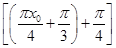
=2
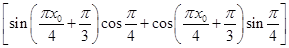
=2 ×
×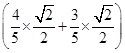 =
=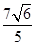 .
.
f(x)=3cos ωx+
 sin ωx=2
sin ωx=2 sin
sin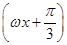 ,
,又正三角形ABC的高为2
 ,从而BC=4,
,从而BC=4,所以函数f(x)的周期T=4×2=8,即
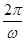 =8,ω=
=8,ω=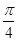 .
.函数f(x)的值域为[-2
 ,2
,2 ].
].(2)因为f(x0)=
 ,由(1)有
,由(1)有f(x0)=2
 sin
sin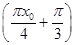 =
= ,
,即sin
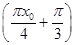 =
=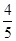
由x0∈
 ,知
,知 ∈
∈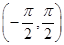 ,
,所以cos
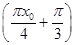 =
= 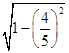 =
=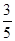 .
.故f(x0+1)=2
 sin
sin
=2
 sin
sin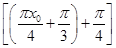
=2

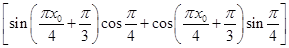
=2
 ×
×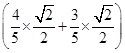 =
=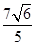 .
.
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目

 的内角
的内角 的对边分别为
的对边分别为 ,且
,且  ,
,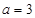 ,求
,求 边上的高的最大值.
边上的高的最大值.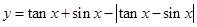 在区间(
在区间( ,
, )内的图象是( )
)内的图象是( )

 ,其部分图象如下图所示,且直线
,其部分图象如下图所示,且直线 与曲线
与曲线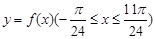 所围成的封闭图形的面积为
所围成的封闭图形的面积为 ,则
,则
 (即
(即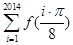 )的值为( )
)的值为( )


 ,函数f(x)=(m+n)·m.
,函数f(x)=(m+n)·m. ,c=4,且f(A)是函数f(x)在
,c=4,且f(A)是函数f(x)在 上的最大值,求△ABC的面积S.
上的最大值,求△ABC的面积S. cos2x的最小正周期和振幅分别是( )
cos2x的最小正周期和振幅分别是( ) 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减,则
上单调递减,则 =
=

 的最小正周期和振幅分别是( )
的最小正周期和振幅分别是( ) ,1
,1 ,1
,1 则
则