题目内容
(2014·保定模拟)若函数f(x)=sin(3x+φ),满足f(a+x)=f(a-x),则f 的值为____________.
的值为____________.
 的值为____________.
的值为____________.0
方法一:易知x=a为对称轴,所以f(a)=sin(3a+φ)=±1,则f =sin
=sin =cos(3a+φ)=0.
=cos(3a+φ)=0.
方法二:因为x=a为对称轴,又f(x)的周期是 ,故x=a+
,故x=a+ 是与x=a相邻的对称轴,而x=a+
是与x=a相邻的对称轴,而x=a+ 是两相邻对称轴中间的f(x)的零点.即f
是两相邻对称轴中间的f(x)的零点.即f =0.
=0.
 =sin
=sin =cos(3a+φ)=0.
=cos(3a+φ)=0.方法二:因为x=a为对称轴,又f(x)的周期是
 ,故x=a+
,故x=a+ 是与x=a相邻的对称轴,而x=a+
是与x=a相邻的对称轴,而x=a+ 是两相邻对称轴中间的f(x)的零点.即f
是两相邻对称轴中间的f(x)的零点.即f =0.
=0.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. 在一个周期内的图像
在一个周期内的图像 上的最大值和最小值.
上的最大值和最小值.
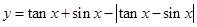 在区间(
在区间( ,
, )内的图象是( )
)内的图象是( )
 sinx﹣cosx,x∈R,若f(x)≥1,则x的取值范围为( )
sinx﹣cosx,x∈R,若f(x)≥1,则x的取值范围为( ) ≤x≤kπ+π,k∈Z}
≤x≤kπ+π,k∈Z} ≤x≤kπ+
≤x≤kπ+ ,k∈Z}
,k∈Z} ≤x≤2kπ+
≤x≤2kπ+ ,k∈Z}
,k∈Z}
 ,满足
,满足 ,
,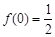 ,则
,则 在区间
在区间 上的最大值与最小值之和为( )
上的最大值与最小值之和为( )



 ,函数f(x)=(m+n)·m.
,函数f(x)=(m+n)·m. ,c=4,且f(A)是函数f(x)在
,c=4,且f(A)是函数f(x)在 上的最大值,求△ABC的面积S.
上的最大值,求△ABC的面积S.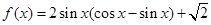 ,
,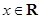 .
.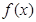 的最小正周期和单调增区间;
的最小正周期和单调增区间;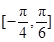 上的最小值和最大值;
上的最小值和最大值;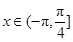 ,求使
,求使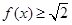 的
的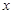 取值范围.
取值范围.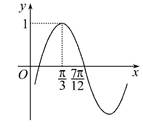
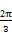
 的最小正周期和振幅分别是( )
的最小正周期和振幅分别是( ) ,1
,1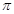 ,1
,1