Question

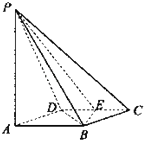
【题目】如图所示，四棱锥P－ABCD的底面ABCD是边长为1的菱形，∠BCD＝60°，E是CD的中点，PA⊥底面ABCD，PA＝.

(1)证明：平面PBE⊥平面PAB；

(2)求二面角A－BE－P的大小．

Answer 1

【答案】（1）见解析（2）60°

【解析】试题分析：（I）连接BD，由已知中四棱锥P﹣ABCD的底面ABCD是边长为1的菱形，∠BCD=60°，E是CD的中点，PA⊥底面ABCD，我们可得BE⊥AB，PA⊥BE，由线面垂直的判定定理可得BE⊥平面PAB，再由面面平行的判定定理可得平面PBE⊥平面PAB；

（II）由（I）知，BE⊥平面PAB，进而PB⊥BE，可得∠PBA是二面角A﹣BE﹣P的平面角．解Rt△PAB即可得到二面角A﹣BE﹣P的大小．

证明：（I）如图所示，连接BD，由ABCD是菱形且∠BCD=60°知，

△BCD是等边三角形．因为E是CD的中点，所以BE⊥CD，又AB∥CD，所以BE⊥AB，

又因为PA⊥平面ABCD，BE平面ABCD，

所以PA⊥BE，而PA∩AB=A，因此 BE⊥平面PAB．

又BE平面PBE，所以平面PBE⊥平面PAB．

解：（II）由（I）知，BE⊥平面PAB，PB平面PAB，所以PB⊥BE．

又AB⊥BE，所以∠PBA是二面角A﹣BE﹣P的平面角．

在Rt△PAB中，．．

故二面角A﹣BE﹣P的大小为60°．