题目内容
【题目】如图，三棱柱A1B1C1-ABC中，侧棱AA1⊥底面ABC，底面三角形ABC是正三角形，E是BC中点，则下列叙述正确的是（ ）
A. AC⊥平面ABB1A1 B. CC1与B1E是异面直线
C. A1C1∥B1E D. AE⊥BB1
【答案】D
【解析】因为三棱柱A1B1C1-ABC中,侧棱AA1⊥底面ABC，底面三角形ABC是正三角形，E是BC中点，
所以对于A,AC与AB夹角为60°,即两直线不垂直，所以. AC不可能垂直于平面ABB1A1；故A错误；
对于B,CC1与B1E都在平面CC1BB1中不平行，故相交；所以B错误；
对于C,A1C1,B1E是异面直线；故C错误；
对于D,因为几何体是三棱柱,并且侧棱AA1⊥底面ABC，底面三角形ABC是正三角形，E是BC中点，所以BB1⊥底面ABC,所以BB1⊥AE,AE⊥BC,得到AE⊥平面BCC1B1,所以AE⊥BB1；
故选：D.
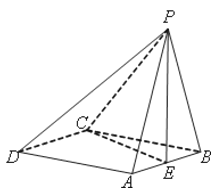
名校通行证有效作业系列答案【题目】如图所示，四棱锥P－ABCD的底面ABCD是边长为1的菱形，∠BCD＝60°，E是CD的中点，PA⊥底面ABCD，PA＝
.
(1)证明：平面PBE⊥平面PAB；
(2)求二面角A－BE－P的大小．
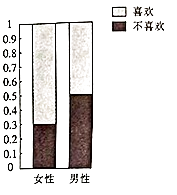
【题目】为了调查喜欢旅游是否与性别有关，调查人员就“是否喜欢旅游”这个问题，在火车站分别随机调研了50名女性和50名男性，根据调研结果得到如图所示的等高条形图
（1）完成下列2×2列联表：
喜欢旅游 | 不喜欢旅游 | 合计 | |
女性 | |||
男性 | |||
合计 |
（2）能否在犯错率不超过0.025的前提下认为“喜欢旅游与性别有关” 附：
P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：K2= 
，其中n=a+b+c+d）