题目内容
【题目】如图是四棱锥的平面展开图,其中四边形ABCD为正方形,E,F,G,H分别为PA,PD,PC,PB的中点,在此几何体中，给出下面四个结论中错误的是（ ）
A. 平面
平面ABCD
B. 直线BE,CF相交于一点
C. EF//平面BGD
D. 
平面BGD
【答案】C
【解析】把图形还原为一个四棱锥,如图所示,
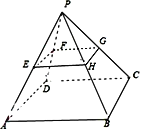
根据三角形中位线的性质，可得
,
平面
平面ABCD，A正确；
在△PAD中,根据三角形的中位线定理可得EF∥AD，
又∵AD∥BC，∴EF∥BC，因此四边形EFBC是梯形，故直线BE与直线CF相交于一点，所以B是正确的；连接AC，设AC中点为M，则M也是BD的中点，因为MG∥PA，且直线MG在平面BDG上，所以有PA∥平面BDG，所以D是正确的；∵EF∥BC，∵EF平面PBC，BC平面PBC，∴直线EF∥平面PBC，再结合图形可得：直线EF与平面BDG不平行，因此C是错误的.
故选C
练习册系列答案
相关题目
