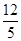题目内容
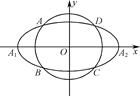
如图,椭圆C0: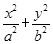 =1(a>b>0,a、b为常数),动圆C1:x2+y2=
=1(a>b>0,a、b为常数),动圆C1:x2+y2=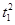 ,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.
,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.
(1)求直线AA1与直线A2B交点M的轨迹方程;
(2)设动圆C2:x2+y2=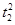 与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明: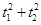 为定值.
为定值.
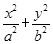 =1(a>b>0,a、b为常数),动圆C1:x2+y2=
=1(a>b>0,a、b为常数),动圆C1:x2+y2=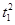 ,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.
,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.
(1)求直线AA1与直线A2B交点M的轨迹方程;
(2)设动圆C2:x2+y2=
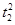 与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明: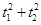 为定值.
为定值.(1) =1(x<-a,y<0).(2)见解析
=1(x<-a,y<0).(2)见解析
 =1(x<-a,y<0).(2)见解析
=1(x<-a,y<0).(2)见解析(1)解:设A(x1,y1),B(x1,-y1),又知A1(-a,0),A2(a,0),
则直线A1A的方程为y= (x+a),①直线A2B的方程为y=
(x+a),①直线A2B的方程为y= (x-a).②
(x-a).②
由①②得y2= (x2-a2).③由点A(x1,y1)在椭圆C0上,故
(x2-a2).③由点A(x1,y1)在椭圆C0上,故 =1.
=1.
从而 =b2
=b2 ,代入③得
,代入③得 =1(x<-a,y<0).
=1(x<-a,y<0).
(2)证明:设A′(x2,y2),由矩形ABCD与矩形A′B′C′D′的面积相等,得4|x1||y1|=4|x2||y2|,故 .因为点A,A′均在椭圆上,所以b2
.因为点A,A′均在椭圆上,所以b2
 =b2
=b2 .由t1≠t2,知x1≠x2,所以
.由t1≠t2,知x1≠x2,所以 =a2,从而
=a2,从而 =b2,因此
=b2,因此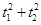 =a2+b2为定值
=a2+b2为定值
则直线A1A的方程为y=
 (x+a),①直线A2B的方程为y=
(x+a),①直线A2B的方程为y= (x-a).②
(x-a).②由①②得y2=
 (x2-a2).③由点A(x1,y1)在椭圆C0上,故
(x2-a2).③由点A(x1,y1)在椭圆C0上,故 =1.
=1.从而
 =b2
=b2 ,代入③得
,代入③得 =1(x<-a,y<0).
=1(x<-a,y<0).(2)证明:设A′(x2,y2),由矩形ABCD与矩形A′B′C′D′的面积相等,得4|x1||y1|=4|x2||y2|,故
 .因为点A,A′均在椭圆上,所以b2
.因为点A,A′均在椭圆上,所以b2
 =b2
=b2 .由t1≠t2,知x1≠x2,所以
.由t1≠t2,知x1≠x2,所以 =a2,从而
=a2,从而 =b2,因此
=b2,因此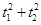 =a2+b2为定值
=a2+b2为定值
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
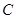 的离心率
的离心率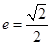 ,长轴的左右端点分别为
,长轴的左右端点分别为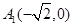 ,
,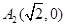 .
.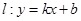 与曲线
与曲线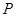 ,且与直线
,且与直线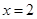 相交于点
相交于点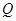 .
.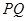 为直径的圆过定点
为直径的圆过定点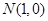 .
.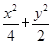 =1的顶点,过坐标原点的直线交椭圆于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连结AC,并延长交椭圆于点B,设直线PA的斜率为k.
=1的顶点,过坐标原点的直线交椭圆于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连结AC,并延长交椭圆于点B,设直线PA的斜率为k.
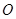 和点
和点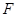 分别为椭圆
分别为椭圆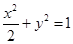 的中心和右焦点,点
的中心和右焦点,点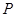 为椭圆上的任意一点,则
为椭圆上的任意一点,则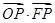 的最小值为( )
的最小值为( )


 +y2=1(a>1)的上顶点为M(0,1),两条过M的动弦MA、MB满足MA⊥MB.
+y2=1(a>1)的上顶点为M(0,1),两条过M的动弦MA、MB满足MA⊥MB. ,求a;
,求a; =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,且过点P
,且过点P ,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
,A为上顶点,F为右焦点.点Q(0,t)是线段OA(除端点外)上的一个动点,
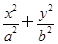 =1(a>b>c>0,a2=b2+c2)的左、右焦点分别为F1,F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且PT的最小值为
=1(a>b>c>0,a2=b2+c2)的左、右焦点分别为F1,F2,若以F2为圆心,b-c为半径作圆F2,过椭圆上一点P作此圆的切线,切点为T,且PT的最小值为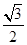 (a-c),则椭圆的离心率e的取值范围是________.
(a-c),则椭圆的离心率e的取值范围是________. 是椭圆
是椭圆 的半焦距,则
的半焦距,则 的取值范围为 .
的取值范围为 .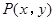 在椭圆
在椭圆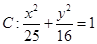 上,
上,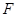 为椭圆
为椭圆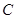 的右焦点,若点
的右焦点,若点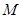 满足
满足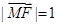 且
且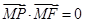 ,则
,则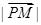 的最小值为( )
的最小值为( )