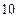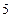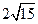题目内容
已知点M(-3,0)、N(3,0)、B(1,0),动圆C与直线MN切于点B,过M、N与圆C相切的两直线相交于点P,则P点的轨迹方程为( )
A.x2-
| B.x2-
| ||||
C.x2+
| D.x2-
|
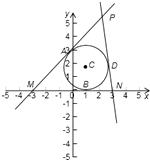
由题意画图如下
可见|MA|=|MB|=4,|ND|=|NB|=2,且|PA|=|PD|,
那么|PM|-|PN|=(|PA|+|MA|)-(|PD|+|ND|)=|MA|-|ND|=4-2=2<|MN|,
所以点P的轨迹为双曲线的右支(右顶点除外),
又2a=2,c=3,则a=1,b2=9-1=8,
所以点P的轨迹方程为x2-
=1(x>1).
故选B.
可见|MA|=|MB|=4,|ND|=|NB|=2,且|PA|=|PD|,
那么|PM|-|PN|=(|PA|+|MA|)-(|PD|+|ND|)=|MA|-|ND|=4-2=2<|MN|,
所以点P的轨迹为双曲线的右支(右顶点除外),
又2a=2,c=3,则a=1,b2=9-1=8,
所以点P的轨迹方程为x2-
| y2 |
| 8 |
故选B.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
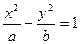 的渐近线方程是
的渐近线方程是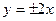
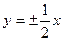
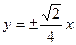

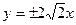
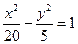 ,那么它的焦距是( )
,那么它的焦距是( )