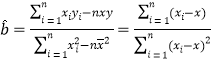题目内容
【题目】已知集合A={x|x2-3x+2≤0},集合B={y|y=x2-2x+a},集合C={x|x2-ax-4≤0}.命题p:A∩B≠;命题q:AC.
(1)若命题p为假命题,求实数a的取值范围;
(2)若命题p∧q为真命题,求实数a的取值范围.
【答案】(1)a>3(2)[0,3].
【解析】解 (1)A=[1,2],B=[a-1,+∞),
若p为假命题,则A∩B=,
故a-1>2,即a>3.
(2)命题p为真,则a≤3.
命题q为真,即转化为当x∈[1,2]时,f(x)=x2-ax-4≤0恒成立,
方法一 ![]() 解得a≥0.
解得a≥0.
方法二 当x∈[1,2]时,a≥x-![]() 恒成立,
恒成立,
而x-![]() 在[1,2]上单调递增,故a≥
在[1,2]上单调递增,故a≥![]() max=0.
max=0.
故实数a的取值范围是[0,3].

练习册系列答案
相关题目