题目内容
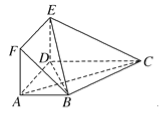
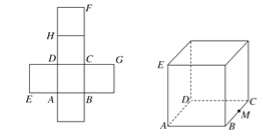
【题目】【2017银川一中高考模拟文】一个正方体的平面展开图及该正方体直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N。
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥平面BDH;
(3)过点M,N,H的平面将正方体分割为两部分,求这两部分的体积比.
【答案】(1)详见解析;(2)详见解析. (3) 3∶1
【解析】 (1)点F,G,H的位置如图所示.

(2)证明:连接BD,设O为BD的中点,连接OM,OH,AC,BH,MN。
∵M,N分别是BC,GH的中点,
∴OM∥CD,且OM=![]() CD,NH∥CD,且NH=
CD,NH∥CD,且NH=![]() CD,
CD,
∴OM∥NH,OM=NH,则四边形MNHO是平行四边形,∴MN∥OH,
又∵MN平面BDH,OH平面BDH,∴MN∥平面BDH。
(3)由(2)知OM∥NH,OM=NH,连接GM,MH,过点M,N,H的平面就是平面GMH,它将正方体分割为两个同高的棱柱,高都是GH,底面分别是四边形BMGF和三角形MGC,
体积比等于底面积之比,即3∶1。

【题目】“开门大吉”是中央电视台推出的娱乐节目.选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌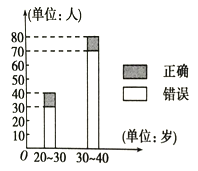
的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参赛选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否的人数如图所示.
(1) 完成下列2×2列联表(见答题纸);
(2)判断是否有90%的把握认为猜对歌曲名称与否和年龄有关;说明你的理由.(下面的临界值表供参考)
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
(参考公式: 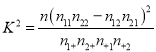 ,
, ![]() )
)
【题目】为了研究某学科成绩(满分100分)是否与学生性别有关,采用分层抽样的方法,从高二年级抽取了30名男生和20名女生的该学科成绩,得到下图所示女生成绩的茎叶图.其中抽取的男生中有21人的成绩在80分以下,规定80分以上为优秀(含80分).
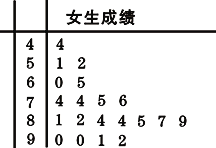
(1)请根据题意,将2×2列联表补充完整;
优秀 | 非优秀 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
(2)据此列联表判断,是否有90%的把握认为该学科成绩与性别有关?
附: 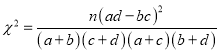 ,其中
,其中![]() .
.
参考数据 | 当 |
当 | |
当 | |
当 |