题目内容
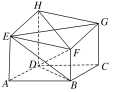
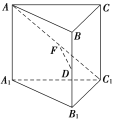
【题目】在棱长均相等的正三棱柱ABCA1B1C1中，D为BB1的中点，F在AC1上，且DF⊥AC1，则下述结论：
①AC1⊥BC；
②AF＝FC1；
③平面DAC1⊥平面ACC1A1，其中正确的个数为( )
A．0 B．1
C．2 D．3
【答案】C
【解析】选C.不妨设棱长为2。①连接AB1，则AB1＝AC1＝2
，∴∠AC1B1≠90°，即AC1与B1C1不垂直，又BC∥B1C1，∴①错；②连接AD，DC1，在△ADC1中，AD＝DC1＝
，而DF⊥AC1，∴F是AC1的中点，∴②对；由②知在△ADC1中DF＝
，连接CF，CD，易知CF＝，而在Rt△CBD中，CD＝，∴DF2＋CF2＝CD2，∴DF⊥CF，又DF⊥AC1，CF∩AC1＝F，
∴DF⊥平面AA1C1C，∴③对，故选C.
练习册系列答案
相关题目
【题目】重庆市某厂党支部10月份开展“两学一做”活动，将10名党员技工平均分为甲，乙两组进行技能比赛．要求在单位时间内每个技工加工零件若干，其中合格零件的个数如下表：
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 4 | 5 | 7 | 9 | 10 |
乙组 | 5 | 6 | 7 | 8 | 9 |
（1）分别求出甲，乙两组技工在单位时间内完成合格零件的平均数及方差，并由此分析两组技工的技术水平；
（2）质检部门从该车间甲，乙两组中各随机抽取1名技工，对其加工的零件进行检测，若两人完成合格零件个数之和超过12件，则称该车间“质量合格”，求该车间“质量合格”的概率．
