题目内容
【题目】如图，已知M(x0，y0)是椭圆C：
＋
＝1上的任一点，从原点O向圆M：(x－x0)2＋(y－y0)2＝2作两条切线，分别交椭圆于点P，Q.
(1)若直线OP，OQ的斜率存在，并记为k1，k2，求证：k1k2为定值；
(2)试问|OP|2＋|OQ|2是否为定值？若是，求出该值；若不是，说明理由．
【答案】见解析
【解析】
解：(1)证明：因为直线OP：y＝k1x，OQ：y＝k2x与圆M相切，所以
＝
，
化简得：(x－2)k－2x0y0k1＋y－2＝0，
同理：(x－2)k－2x0y0k2＋y－2＝0，
所以k1，k2是方程(x－2)k2－2x0y0k＋y－2＝0的两个不相等的实数根，
所以k1·k2＝
.
因为点M(x0，y0)在椭圆C上，所以
＋
＝1，即y＝3－
x，
所以k1k2＝
＝－为定值．
(2)|OP|2＋|OQ|2是定值，定值为9.
理由如下：
方法一：①当直线OP，OQ不落在坐标轴上时，设P(x1，y1)，Q(x2，y2)，
联立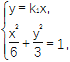
解得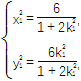
所以x＋y＝
，同理得x＋y＝
，
又因为k1k2＝－，
所以|OP|2＋|OQ|2＝x＋y＋x＋y
＝＋
＝＋
＝
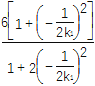
＝9.
②当直线OP，OQ落在坐标轴上时，显然有|OP|2＋|OQ|2＝9，
综上：|OP|2＋|OQ|2＝9为定值．
方法二：①当直线OP，OQ不落在坐标轴上时，设P(x1，y1)，Q(x2，y2)，
因为k1k2＝－，所以yy＝
xx，
因为P(x1，y1)，Q(x2，y2)在椭圆C上，
所以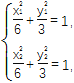
即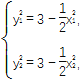
所以
＝xx，整理得x＋x＝6，
所以y＋y＝＋＝3，所以|OP|2＋|OQ|2＝9.
②当直线OP，OQ落在坐标轴上时，显然有|OP|2＋|OQ|2＝9，
综上：|OP|2＋|OQ|2＝9为定值．
练习册系列答案
相关题目
