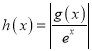题目内容
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 的周期为
的周期为![]() ;
;
②![]() 在
在![]() 上单调递增;
上单调递增;
③函数![]() 在
在![]() 上有
上有![]() 个零点;
个零点;
④函数![]() 的最小值为
的最小值为![]() .
.
其中所有正确结论的编号为( )
A.①②B.②③C.③④D.②④
【答案】C
【解析】
利用特殊值法可判断①的正误;当![]() 时,化简函数
时,化简函数![]() 的解析式,利用整体代入法验证函数
的解析式,利用整体代入法验证函数![]() 在区间
在区间![]() 上的单调性,可判断②的正误;求得方程
上的单调性,可判断②的正误;求得方程![]() 在区间
在区间![]() 上的实数解,可判断③的正误;分别求出函数
上的实数解,可判断③的正误;分别求出函数![]() 在区间
在区间![]() 和
和![]() 上的最小值,比较大小后可判断④的正误.综合可得出结论.
上的最小值,比较大小后可判断④的正误.综合可得出结论.
对于①,![]() ,
,![]() ,
,
![]() ,
,![]() ,所以,函数
,所以,函数![]() 的周期不是
的周期不是![]() ,命题①错误;
,命题①错误;
对于②,当![]() 时,
时,![]() ,则
,则![]() ,
,
所以,函数![]() 在区间
在区间![]() 上不单调,命题②错误;
上不单调,命题②错误;
对于③,![]() ,
,
且该函数的定义域为![]() ,则函数
,则函数![]() 为偶函数,
为偶函数,
当![]() 时,
时,![]() ,
,![]() ,
,
令![]() ,可得
,可得![]() 或
或![]() ,解得
,解得![]() 或
或![]() ,
,
由于函数![]() 为偶函数,则方程
为偶函数,则方程![]() 在区间
在区间![]() 上的实根为
上的实根为![]() .
.
所以,函数![]() 在
在![]() 上有
上有![]() 个零点,命题③正确;
个零点,命题③正确;
对于④,当![]() 时,
时,![]() ,
,
所以,函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
由于函数![]() 为
为![]() 上的增函数,则该函数在
上的增函数,则该函数在![]() 上的最小值为
上的最小值为![]() .
.
因此,函数![]() 的最小值为
的最小值为![]() ,命题④正确.
,命题④正确.
故选:C.

 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案【题目】某市环保部门对该市市民进行了一次垃圾分类知识的网络问卷调查,每位市民仅有一次参加机会,通过随机抽样,得到参与问卷调查的100人的得分(满分:100分)数据,统计结果如表所示:
组别 |
|
|
|
|
|
|
男 | 2 | 3 | 5 | 15 | 18 | 12 |
女 | 0 | 5 | 10 | 10 | 7 | 13 |
(1)若规定问卷得分不低于70分的市民称为“环保关注者”,请完成答题卡中的![]() 列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否为“环保关注者”与性别有关?
列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否为“环保关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环保达人”.视频率为概率.
①在我市所有“环保达人”中,随机抽取3人,求抽取的3人中,既有男“环保达人”又有女“环保达人”的概率;
②为了鼓励市民关注环保,针对此次的调查制定了如下奖励方案:“环保达人”获得两次抽奖活动;其他参与的市民获得一次抽奖活动.每次抽奖获得红包的金额和对应的概率.如下表:
红包金额(单位:元) | 10 | 20 |
概率 |
|
|
现某市民要参加此次问卷调查,记![]() (单位:元)为该市民参加间卷调查获得的红包金额,求
(单位:元)为该市民参加间卷调查获得的红包金额,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |