题目内容
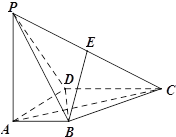
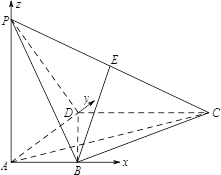
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.
(1)证明:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)若![]() 为棱
为棱![]() 上一点,满足
上一点,满足![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)可以建立空间直角坐标系,利用向量数量积来证明![]() ,;(2)向量法:先求平面
,;(2)向量法:先求平面![]() 的法向量
的法向量![]() ,然后利用公式
,然后利用公式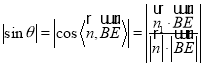 求直线
求直线![]() 与平面
与平面![]() 所成角的正弦值;(3)向量法:先求平面
所成角的正弦值;(3)向量法:先求平面![]() 和平面
和平面![]() 的法向量
的法向量![]() ,再利用公式
,再利用公式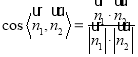 来求二面角
来求二面角![]() 的余弦值.
的余弦值.
依题意,以点![]() 为原点建立空间直角坐标系(如图),可得
为原点建立空间直角坐标系(如图),可得![]() ,
,![]() ,由点
,由点![]() 为棱
为棱![]() 的中点,得
的中点,得![]() .
.
(1)向量![]() ,
,![]() ,故
,故![]() . ∴
. ∴![]() .
.
(2)向量![]() ,设
,设![]() 为平面
为平面![]() 的法向量,则
的法向量,则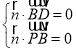 ,即
,即![]() ,
,
不妨令![]() ,可得
,可得![]() 为平面
为平面![]() 的一个法向量.
的一个法向量.
于是有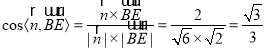 ,
,
∴直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(3)![]() ,
,
由点![]() 在棱
在棱![]() 上,故
上,故![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() ,即
,即![]() .
.
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则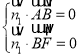 ,即
,即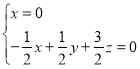 ,不妨令
,不妨令![]() ,可得
,可得![]() 为平面
为平面![]() 的一个法向量.取平面
的一个法向量.取平面![]() 的法向量
的法向量![]() ,则
,则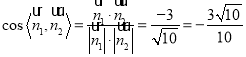 .
.
易知,二面角![]() 是锐角,∴其余弦值为
是锐角,∴其余弦值为![]() .
.

 每课必练系列答案
每课必练系列答案【题目】“中国式过马路”存在很大的交通安全隐患,某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如图的![]() 列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是![]() .
.
(1)求![]() 列联表中的
列联表中的![]() ,
,![]() 的值;
的值;
男性 | 女性 | 合计 | |
反感 | 10 |
|
|
不反感 |
| 8 |
|
合计 |
|
| 30 |
(2)根据列联表中的数据,判断是否有95%把握认为反感“中国式过马路”与性别有关?
临界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式: ,
,![]()
【题目】某校在高一部分学生中调查男女同学对某项体育运动的喜好情况,其二维条形图如图(黑色代表喜好,白色代表不喜好).
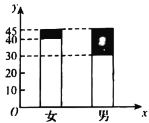
(1)写出![]() 列联表;
列联表;
(2)能否有99%的把握认为喜好这项体育运动与性别有关;
(3)在这次调查中从喜好这项体育活动的一名男生和两名女生中任选两人进行专业培训,求恰是一男一女的概率.
附: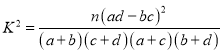
| 0.25 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.83 |