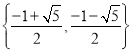题目内容
【题目】已知数集![]() 具有性质
具有性质![]() ;对任意的
;对任意的![]() 、
、![]() ,
,![]() ,与
,与![]() 两数中至少有一个属于
两数中至少有一个属于![]() .
.
(1)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)证明:![]() ,且
,且![]() ;
;
(3)当![]() 时,若
时,若![]() ,求集合
,求集合![]() .
.
【答案】(1) 集合![]() 具有性质
具有性质![]() ,集合
,集合![]() 不具有性质
不具有性质![]() .(2)证明见解析.(3)
.(2)证明见解析.(3)![]() .
.
【解析】
(1)利用![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() .即可判断出结论.
.即可判断出结论.
(2)令“![]() ,由“
,由“![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() ”可得
”可得![]() 属于
属于![]() .
.
令![]() ,那么
,那么![]() 是集合
是集合![]() 中某项,
中某项,![]() 不符合不符合题意,
不符合不符合题意,![]() 符合.同理可得:令
符合.同理可得:令![]() 可以得到
可以得到![]() ,令
,令![]() ,
,![]() 可以得到
可以得到![]() ,倒序相加即可.
,倒序相加即可.
(3)当![]() 时,取
时,取![]() ,当
,当![]() 时,
时,![]() ,由A具有性质P,
,由A具有性质P,![]() ,又
,又![]() 时,
时,![]() ,可得
,可得![]()
![]() ,则
,则![]() ,又
,又![]() ,可得
,可得![]() ,则
,则![]() ,则有
,则有![]() .可得即
.可得即![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 等差数列是首项为0,公差为
等差数列是首项为0,公差为![]() 等差数列.
等差数列.
解:(1)在集合![]() 中,设
中,设![]()
①![]() ,具有性质
,具有性质![]()
②![]() ,具有性质
,具有性质![]()
③![]() ,具有性质
,具有性质![]()
④![]() ,具有性质
,具有性质![]()
⑤![]() ,具有性质
,具有性质![]()
⑥![]() ,具有性质
,具有性质![]()
综上所述:集合![]() 具有性质
具有性质![]() ;
;
在集合![]() 中,设
中,设![]() ,
,
①![]() ,具有性质
,具有性质![]()
②![]() ,具有性质
,具有性质![]()
③![]() ,具有性质
,具有性质![]()
④![]() ,不具有性质
,不具有性质![]()
⑤![]() ,具有性质
,具有性质![]()
⑥![]() ,具有性质
,具有性质![]()
综上所述:集合![]() 不具有性质
不具有性质![]() .
.
故集合![]() 具有性质
具有性质![]() ,集合
,集合![]() 不具有性质
不具有性质![]() .
.
(2) 证明:令![]()
![]() ,
,
则![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() ”,
”,
![]() 不属于
不属于![]() ,
,![]() 属于
属于![]() .
.
令![]() ,那么
,那么![]() 是集合
是集合![]() 中某项,
中某项,![]() 不符合题意,
不符合题意,![]() 可以.
可以.
如果是![]() 或者
或者![]() ,那么可知
,那么可知![]() ,
,
那么![]() ,只能是等于
,只能是等于![]() ,矛盾.
,矛盾.
所以令![]() 可以得到
可以得到![]() ,
,
同理,令![]() ,
,![]() 可以得到
可以得到![]() ,
,
![]() 倒序相加即可得到
倒序相加即可得到![]()
即![]()
(3)当![]() 时,取
时,取![]() ,当
,当![]() 时,
时,![]() ,
,
由![]() 具有性质
具有性质![]() ,
,![]() ,又
,又![]() 时,
时,![]() ,
,
![]()
![]() ,
,
![]() ,
,
则![]() ,
,
![]() ,
,
从而可得![]() ,
,
故![]() ,即
,即![]() ,
,
又![]()
![]()
,则![]() ,则有
,则有![]()
又![]()
![]() ,
,
即![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 等差数列,
等差数列,
![]()

练习册系列答案
相关题目