Question

【题目】已知矩形ABCD中，AB＝2，BC＝1，F为线段CD上一动点（不含端点），现将△ADF沿直线AF进行翻折，在翻折过程中不可能成立的是（　　）

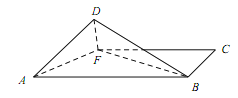
A.存在某个位置，使直线AF与BD垂直B.存在某个位置，使直线AD与BF垂直

C.存在某个位置，使直线CF与DA垂直D.存在某个位置，使直线AB与DF垂直

Answer 1

【答案】C

【解析】

连结BD，在中，可以作于O，并延长交CD于F，得到成立，得到A正确；由翻折中，保持不变，可得到B正确；根据翻折过程中，，可得到C错误；根据翻折过程中，保持不变，假设成立，得到平面ABD，结合题中条件，进而可得出结果.

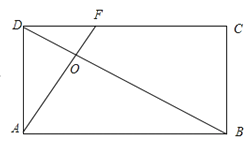
对于A，连结BD，在中，可以作于O，并延长交CD于F，

则成立，翻折过程中，这个垂直关系保持不变，故A正确；

对于B，在翻折过程中，保持不变，

当时，有平面，从而，

此时，AD＝1，AB＝2，BD＝，故B正确；

对于C，在翻折过程中，保持不变，若成立，则平面CDF，从而，

AD＝1，AC＝，得CD＝2，

在翻折过程中，，即CD＜2，所以，CD＝2不成立，C不正确；

对于D，在翻折过程中，保持不变，若成立，则平面ABD，从而，

设此时，则BF＝，

BD＝，只要，BD就存在，

所以D正确

选C。