题目内容
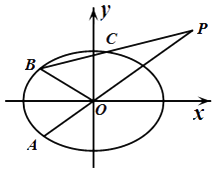
【题目】已知椭圆 ![]() =1(a>b>0)的右焦点为F1(1,0),离心率为e.设A,B为椭圆上关于原点对称的两点,AF1的中点为M,BF1的中点为N,原点O在以线段MN为直径的圆上.若直线AB的倾斜角α∈(0,
=1(a>b>0)的右焦点为F1(1,0),离心率为e.设A,B为椭圆上关于原点对称的两点,AF1的中点为M,BF1的中点为N,原点O在以线段MN为直径的圆上.若直线AB的倾斜角α∈(0, ![]() ),则e的取值范围是 .
),则e的取值范围是 .
【答案】[ ![]() ﹣1,1)
﹣1,1)
【解析】解:由椭圆 ![]() =1(a>b>0)的焦点在x轴上,记线段MN与x轴交点为C,由AF1的中点为M,BF1的中点为N,
=1(a>b>0)的焦点在x轴上,记线段MN与x轴交点为C,由AF1的中点为M,BF1的中点为N,
∴MN∥AB,|F1C|=|CO|= ![]() ,
,
∵A、B为椭圆上关于原点对称的两点,
∴|CM|=|CN|.
∵原点O在以线段MN为直径的圆上,
∴|CO|=|CM|=|CN|= ![]() .
.
∴|OA|=|OB|=c=1.
∵|OA|>b,
∴a2=b2+c2<2c2 ,
∴e= ![]() >
> ![]() .
.
设A(x,y),
由 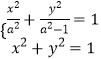 ,
,
解得: 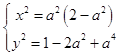 .
.
AB的倾斜角α∈(0, ![]() ),
),
∴直线AB斜率为0<k≤ ![]() ,
,
∴0< 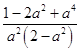 ≤3,
≤3,
∴1﹣ ![]() ≤a2≤1+
≤a2≤1+ ![]() ,
,
即为 ![]() ≤a≤
≤a≤ ![]() ,
,
∴e= ![]() =
= ![]() ∈[
∈[ ![]() ﹣1,
﹣1, ![]() +1],
+1],
由于0<e<1,
∴离心率e的取值范围为[ ![]() ﹣1,1).
﹣1,1).
所以答案是:[ ![]() ﹣1,1).
﹣1,1).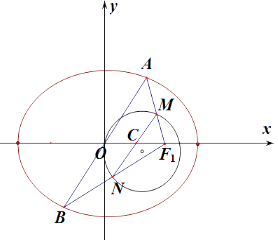

练习册系列答案
相关题目