Question

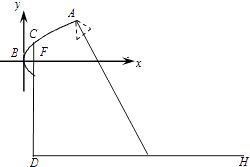
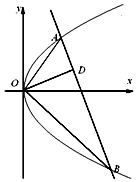
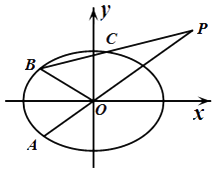
【题目】如图，在平面直角坐标系xOy中，已知椭圆 =1（a＞b＞0）的离心率为 ．A为椭圆上异于顶点的一点，点P满足 = ，

（1）若点P的坐标为（2， ），求椭圆的方程；
（2）设过点P的一条直线交椭圆于B，C两点，且 =m ，直线OA，OB的斜率之积﹣ ，求实数m的值；
（3）在（1）的条件下，是否存在定圆M，使得过圆M上任意一点T都能作出该椭圆的两条切线，且这两条切线互相垂直？若存在，求出定圆M；若不存在，说明理由．

Answer 1

【答案】
（1）解：由P（2， ），设A（x，y），则 =（2， ）， =（﹣x，﹣y），

由题意可知： = ，

∴ ，则 ，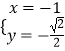

A（﹣1，﹣ ），代入椭圆方程，得 ，

又椭圆的离心率e= = ，

则 = ，②

由①②，得a2=2，b2=1，

故椭圆的方程为

（2）解：设A（x1，y1），B（x2，y2），C（x3，y3），

∵ = ，

∴P（﹣2x1，﹣2y1），．

∵ =m ，

∴（﹣2x1﹣x2，﹣2y1﹣y2）=m（x3﹣x2，y3﹣y2），

即 ，

于是 ．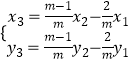

代入椭圆方程，得 + =1，

（ ）+ （ ）﹣ （ + ）=1，

∵A，B在椭圆上， ， ，

由直线OA，OB的斜率之积﹣ ，即 =﹣

∴ ，

∴ ，解得：m=

（3）解：存在定圆M，x2+y2=3，

在定圆M上任取一点T（x0，y0），其中x0≠± ，

设过点T（x0，y0）的椭圆的切线方程为y﹣y0=k（x﹣y0），即y=kx﹣kx0+y0，

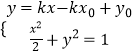∴ ，整理得：（1+2k2）x2﹣4k（﹣kx0+y0）x+2（﹣kx0+y0）2﹣2=0，

由△=16k2（﹣kx0+y0）2﹣8（1+2k2）[（﹣kx0+y0）2﹣1]=0，

整理得：（2﹣ ）k2+2kx0y0+1﹣ =0

故过点T（x0，y0）的椭圆的两条切线斜率k1，k2分别是（2﹣ ）k2+2kx0y0+1﹣ =0的两解．

故k1k2= = = =﹣1，

∴椭圆的两条切线垂直．

当x0=± 时，

显然存在两条互相垂直的切线

【解析】（1）由题意可知： = ，求得A点坐标，由e= = ，将A代入椭圆方程，即可求得a和b的值，求得椭圆的方程；（2）设A（x1 ， y1），B（x2 ， y2），C（x3 ， y3），根据 =m ，求得 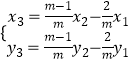．代入椭圆方程 + =1，由直线OA，OB的斜率之积﹣ ，利用斜率公式求得 ，代入整理得： ，解得：m= ，；（3）假设存在否存在定圆M，求得直线的切线方程，代入椭圆方程，由△=0，求得（2﹣ ）k2+2kx0y0+1﹣ =0，则椭圆的两条切线斜率k1 ， k2分别是（2﹣ ）k2+2kx0y0+1﹣ =0的两解，由韦达定理求得k1k2= = = =﹣1，因此椭圆的两条切线垂直，则当x0=± 时，显然存在两条互相垂直的切线，即可求得圆的方程．