题目内容
【题目】如图,某大型景区有两条直线型观光路线![]() ,
, ![]() ,
,![]() ,点
,点![]() 位于
位于![]() 的平分线上,且与顶点
的平分线上,且与顶点![]() 相距1公里.现准备过点
相距1公里.现准备过点![]() 安装一直线型隔离网
安装一直线型隔离网![]() (
(![]() 分别在
分别在![]() 和
和![]() 上),围出三角形区域
上),围出三角形区域![]() ,且
,且![]() 和
和![]() 都不超过5公里.设
都不超过5公里.设![]() ,
, ![]() (单位:公里).
(单位:公里).
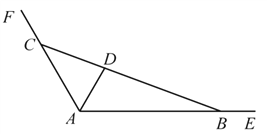
(Ⅰ)求![]() 的关系式;
的关系式;
(Ⅱ)景区需要对两个三角形区域![]() ,
, ![]() 进行绿化.经测算,
进行绿化.经测算, ![]() 区城每平方公里的绿化费用是
区城每平方公里的绿化费用是![]() 区域的两倍,试确定
区域的两倍,试确定![]() 的值,使得所需的总费用最少.
的值,使得所需的总费用最少.
【答案】(Ⅰ)![]() ;(Ⅱ)当
;(Ⅱ)当![]() ,
, ![]() (单位:公里)时,所需的总费用最少..
(单位:公里)时,所需的总费用最少..
【解析】试题分析:(Ⅰ) 由题意得![]() ,利用面积公式及条件可得
,利用面积公式及条件可得![]() (其中
(其中![]() );
);
(Ⅱ)设![]() 区域每平方公里的绿化费用为
区域每平方公里的绿化费用为![]() (
(![]() 为常数),两区域总费用为
为常数),两区域总费用为![]() ,则有
,则有![]() ,记
,记![]() ,由(Ⅰ)可知
,由(Ⅰ)可知![]() ,即
,即![]() ,
, ![]() 用均值不等式求最值即可.
用均值不等式求最值即可.
试题解析:
(Ⅰ)解法一:由题意得![]() ,
,
故![]() ,
,
即![]() ,
,
所以![]() (其中
(其中![]() ).
).
解法二:在![]() 中,由余弦定理得:
中,由余弦定理得: ![]() ,
,
则![]() ,同理可得
,同理可得![]() ,
,
在![]() 中,由正弦定理得:
中,由正弦定理得: ![]() ,
,
在![]() 中,由正弦定理得:
中,由正弦定理得: ![]() ,
,
因为![]() ,两式相除可得
,两式相除可得![]() ,
,
化简得![]() (其中
(其中![]() ,
, ![]() ).
).
(Ⅱ)设![]() 区域每平方公里的绿化费用为
区域每平方公里的绿化费用为![]() (
(![]() 为常数),两区域总费用为
为常数),两区域总费用为![]() ,
,
则有![]() ,
,
记![]() ,由(Ⅰ)可知
,由(Ⅰ)可知![]() ,即
,即![]() ,
,
则![]() ,
,
当且仅当![]() ,即
,即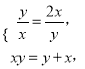 解得
解得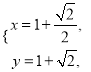 此时等号成立.
此时等号成立.
答:当![]() ,
, ![]() (单位:公里)时,所需的总费用最少.
(单位:公里)时,所需的总费用最少.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目