题目内容
设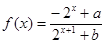 (
(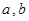 为实常数).
为实常数).
(1)当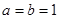 时,证明:
时,证明: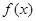 不是奇函数;
不是奇函数;
(2)设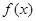 是奇函数,求
是奇函数,求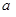 与
与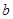 的值;
的值;
(3)在满足(2)且当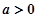 时,若对任意的
时,若对任意的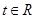 ,不等式
,不等式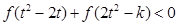
恒成立,求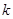 的取值范围.
的取值范围.
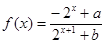 (
(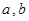 为实常数).
为实常数).(1)当
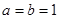 时,证明:
时,证明: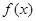 不是奇函数;
不是奇函数;(2)设
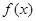 是奇函数,求
是奇函数,求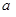 与
与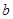 的值;
的值;(3)在满足(2)且当
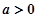 时,若对任意的
时,若对任意的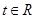 ,不等式
,不等式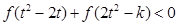
恒成立,求
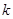 的取值范围.
的取值范围. (1)见解析 (2) 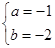 或
或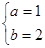 (3)
(3)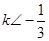
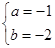 或
或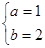 (3)
(3)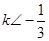
本试题主要是考查了函数的奇偶性和函数的单调性的运用。
(1)举出反例即可. ,
,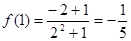 ,
,
 ,所以
,所以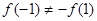 ,
,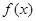 不是奇函数
不是奇函数
(2)当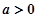 时得知
时得知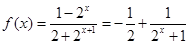 ,利用定义法证明单调性。然后得到
,利用定义法证明单调性。然后得到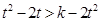 .即对一切
.即对一切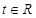 有:
有:
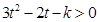 ,从而借助于判别式得到。
,从而借助于判别式得到。
解:(1)举出反例即可. ,
,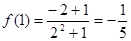 ,
,
 ,所以
,所以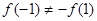 ,
,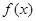 不是奇函数;…………4分
不是奇函数;…………4分
(2)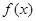 是奇函数时,
是奇函数时,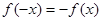 ,即
,即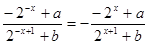 对定义域内任意实数
对定义域内任意实数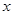 成立.…………5分
成立.…………5分
化简整理得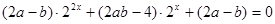 ,这是关于
,这是关于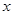 的恒等式,所以
的恒等式,所以
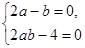 所以
所以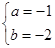 或
或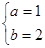 . 经检验都符合题意.…………8分
. 经检验都符合题意.…………8分
(3)由当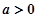 时得知
时得知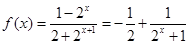 ,
,
设
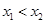 则
则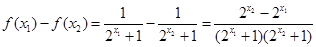
因为函数y=2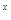 在R上是增函数且
在R上是增函数且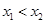 ∴
∴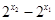 >0
>0
又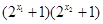 >0 ∴
>0 ∴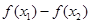 >0即
>0即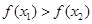
∴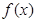 在
在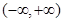 上为减函数。 ……………11分
上为减函数。 ……………11分
因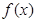 是奇函数,从而不等式:
是奇函数,从而不等式: 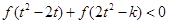
等价于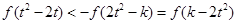 ,
,
因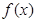 为减函数,由上式推得:
为减函数,由上式推得: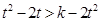 .即对一切
.即对一切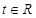 有:
有:
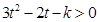 ,
,
从而判别式 ……….14分
……….14分
(1)举出反例即可.
 ,
,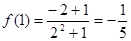 ,
, ,所以
,所以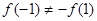 ,
,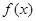 不是奇函数
不是奇函数(2)当
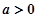 时得知
时得知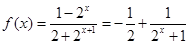 ,利用定义法证明单调性。然后得到
,利用定义法证明单调性。然后得到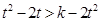 .即对一切
.即对一切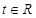 有:
有: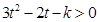 ,从而借助于判别式得到。
,从而借助于判别式得到。解:(1)举出反例即可.
 ,
,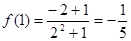 ,
, ,所以
,所以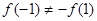 ,
,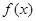 不是奇函数;…………4分
不是奇函数;…………4分(2)
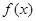 是奇函数时,
是奇函数时,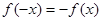 ,即
,即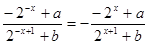 对定义域内任意实数
对定义域内任意实数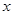 成立.…………5分
成立.…………5分化简整理得
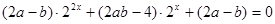 ,这是关于
,这是关于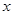 的恒等式,所以
的恒等式,所以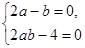 所以
所以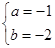 或
或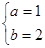 . 经检验都符合题意.…………8分
. 经检验都符合题意.…………8分(3)由当
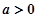 时得知
时得知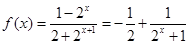 ,
,设

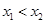 则
则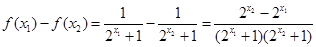
因为函数y=2
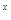 在R上是增函数且
在R上是增函数且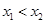 ∴
∴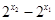 >0
>0又
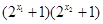 >0 ∴
>0 ∴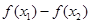 >0即
>0即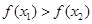
∴
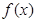 在
在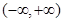 上为减函数。 ……………11分
上为减函数。 ……………11分因
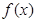 是奇函数,从而不等式:
是奇函数,从而不等式: 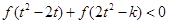
等价于
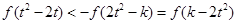 ,
,因
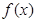 为减函数,由上式推得:
为减函数,由上式推得: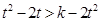 .即对一切
.即对一切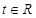 有:
有: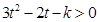 ,
, 从而判别式
 ……….14分
……….14分
练习册系列答案
相关题目
 -
- 的上确界为( )
的上确界为( )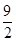
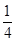
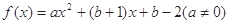 ,若存在实数
,若存在实数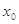 ,使
,使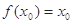 成立,则称
成立,则称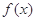 的不动点.
的不动点.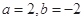 时,求
时,求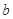 ,函数
,函数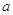 的取值范围;
的取值范围;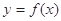 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数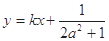 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.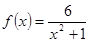
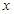 的不等式
的不等式 的解集一切实数,求实数
的解集一切实数,求实数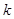 的取值范围;
的取值范围;
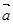 ="(1,2),"
="(1,2)," 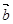 =(-2,1),k,t为正实数,向量
=(-2,1),k,t为正实数,向量  =
= 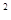 +1)
+1)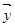 =-k
=-k
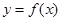 的周期为2,当
的周期为2,当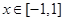 时
时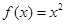 ,那么函数
,那么函数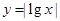 的图象的交点共有
的图象的交点共有 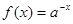
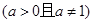 ,且
,且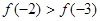 ,则
,则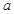 的取值范围是( )
的取值范围是( )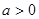
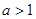
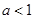
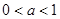
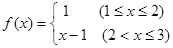 ,
,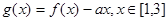 ,其中
,其中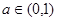 ,记函数
,记函数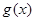 的最大值与最小值的差为
的最大值与最小值的差为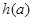 ,则
,则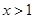 ,则函数
,则函数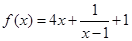 的最小值是( )
的最小值是( )