题目内容
原点为顶点,坐标轴为对称轴,且焦点在直线x-2y-4=0上的抛物线方程为.
x2=-8y或y2=16x
当对称轴为x轴,则焦点坐标为(4,0),即p=8.故抛物线方程为y2=16x.
当对称轴为y轴,则焦点坐标为(0,-2),即p=4.故抛物线方程为x2=-8y.
综上,所求抛物线的方程为y2=16x或x2=-8y.
当对称轴为y轴,则焦点坐标为(0,-2),即p=4.故抛物线方程为x2=-8y.
综上,所求抛物线的方程为y2=16x或x2=-8y.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
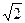
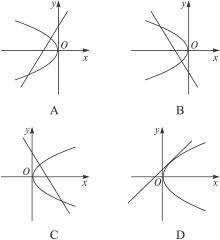
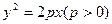 上一定点
上一定点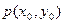
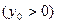 ,作直线分别交抛物线于
,作直线分别交抛物线于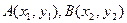
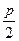 的点到焦点
的点到焦点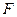 的距离;
的距离;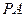 与
与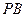 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求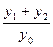 的值,并证明直线
的值,并证明直线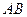 的斜率是非零常数。
的斜率是非零常数。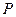 是抛物线
是抛物线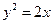 上的动点,焦点为
上的动点,焦点为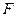 ,点
,点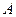 的坐标是
的坐标是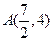 ,则
,则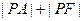 的最小值是( )
的最小值是( )