题目内容
已知直线l:y=kx+2与抛物线y2=2x交于A、B两点,AB的中点的纵坐标为-2,则直线l与直线3x-y+2=0的夹角为___________.
arctan7
将x=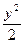 代入y=kx+2,得
代入y=kx+2,得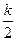 y2-y+2=0.
y2-y+2=0.
∴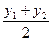 =
=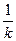 =-2.∴k=-
=-2.∴k=-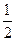 .
.
∴所求的夹角α的正切值为tanα=|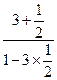 |=7.∴α=arctan7.
|=7.∴α=arctan7.
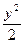 代入y=kx+2,得
代入y=kx+2,得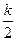 y2-y+2=0.
y2-y+2=0.∴
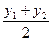 =
=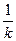 =-2.∴k=-
=-2.∴k=-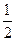 .
.∴所求的夹角α的正切值为tanα=|
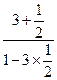 |=7.∴α=arctan7.
|=7.∴α=arctan7.
练习册系列答案
相关题目
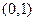 与抛物线
与抛物线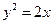 有且只有一个公共点的直线的条数是( )
有且只有一个公共点的直线的条数是( )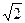
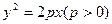 上一定点
上一定点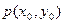
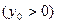 ,作直线分别交抛物线于
,作直线分别交抛物线于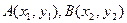
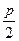 的点到焦点
的点到焦点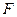 的距离;
的距离;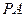 与
与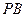 的斜率存在且倾斜角互补时,求
的斜率存在且倾斜角互补时,求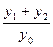 的值,并证明直线
的值,并证明直线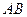 的斜率是非零常数。
的斜率是非零常数。