题目内容
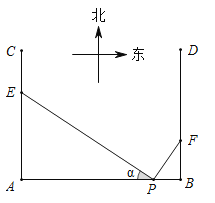
【题目】如图,在P地正西方向8km的A处和正东方向1km的B处各有一条正北方向的公路AC和BD,现计划在AC和BD路边各修建一个物流中心E和F,为缓解交通压力,决定修建两条互相垂直的公路PE和PF,设![]()
![]() Ⅰ
Ⅰ![]() 为减少对周边区域的影响,试确定E,F的位置,使
为减少对周边区域的影响,试确定E,F的位置,使![]() 与
与![]() 的面积之和最小;
的面积之和最小;
![]() Ⅱ
Ⅱ![]() 为节省建设成本,求使
为节省建设成本,求使![]() 的值最小时AE和BF的值.
的值最小时AE和BF的值.
【答案】(1) 当![]() km,
km,![]() km时,
km时,![]() 与
与![]() 的面积之和最小.
的面积之和最小.
(2) 当![]() 为
为![]() ,且
,且![]() 为
为![]() 时,
时,![]() 的值最小.
的值最小.
【解析】
试题分析:(1)用角![]() 表示
表示![]() ,从而表示三角形
,从而表示三角形![]() 的面积,求出面积之和用基本不等式求最小值,求出等号成立时的
的面积,求出面积之和用基本不等式求最小值,求出等号成立时的![]() ,即可确定
,即可确定![]() 的位置;
的位置;
(2) 用角![]() 表示
表示![]() ,构建函数
,构建函数![]() ,用导数与最值的关系求之即可.
,用导数与最值的关系求之即可.
试题解析:(1)在Rt△PAE中,由题意可知![]() ,AP=8,则
,AP=8,则![]() .
.
所以![]() . 2分
. 2分
同理在Rt△PBF中,![]() ,PB=1,则
,PB=1,则![]() ,
,
所以![]() . 4分
. 4分
故△PAE与△PFB的面积之和为![]() 5分
5分
![]() =8,
=8,
当且仅当![]() ,即
,即![]() 时,取“=”,
时,取“=”,
故当![]() km,
km,![]() km时,
km时,![]() 与
与![]() 的面积之和最小. 6分
的面积之和最小. 6分
(2)在Rt△PAE中,由题意可知![]() ,则
,则![]() .
.
同理在Rt△PBF中,![]() ,则
,则![]() .
.
令![]() ,
,![]() , 8分
, 8分
则![]() , 10分
, 10分
令![]() ,得
,得![]() ,记
,记![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 单调减;
单调减;
当![]() 时,
时,![]() ,
,![]() 单调增.
单调增.
所以![]() 时,
时,![]() 取得最小值, 12分
取得最小值, 12分
此时![]() ,
,![]() .
.
所以当![]() km,且
km,且![]() km时,PE+PF的值最小. 14分
km时,PE+PF的值最小. 14分

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目