题目内容
(本题12分)已知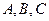 是椭圆
是椭圆 上的三点,其中点
上的三点,其中点 的坐标为
的坐标为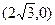 ,
, 过椭圆
过椭圆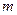 的中心,且
的中心,且 .
.
(1)求椭圆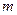 的方程;
的方程;
(2)过点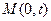 的直线
的直线 (斜率存在时)与椭圆
(斜率存在时)与椭圆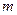 交于两点
交于两点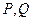 ,设
,设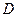 为椭圆
为椭圆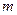 与
与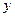 轴负半轴的交点,且
轴负半轴的交点,且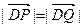 .求实数
.求实数 的取值范围
的取值范围
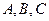 是椭圆
是椭圆 上的三点,其中点
上的三点,其中点 的坐标为
的坐标为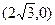 ,
, 过椭圆
过椭圆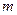 的中心,且
的中心,且 .
.(1)求椭圆
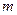 的方程;
的方程;(2)过点
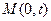 的直线
的直线 (斜率存在时)与椭圆
(斜率存在时)与椭圆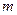 交于两点
交于两点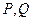 ,设
,设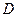 为椭圆
为椭圆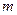 与
与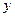 轴负半轴的交点,且
轴负半轴的交点,且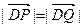 .求实数
.求实数 的取值范围
的取值范围(1)椭圆m: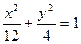
(2)t∈(-2,4)
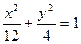
(2)t∈(-2,4)
解(1)∵ 过(0,0)
过(0,0)
则
∴∠OCA=90°, 即 …………2分
…………2分
又∵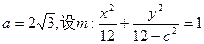
将C点坐标代入得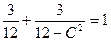
解得 c2=8,b2=4
 ∴椭圆m:
∴椭圆m: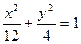 …………4分
…………4分
(2)由条件D(0,-2) ∵M(0,t)
1°当k=0时,显然-2<t<2 …………6分
2°当k≠0时,设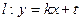
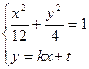 消y得
消y得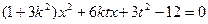 …………8分
…………8分
由△>0 可得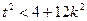 ①………………9分
①………………9分
设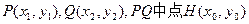
则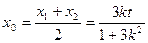
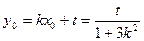
∴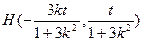 …………11分
…………11分
由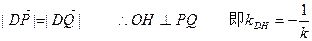
∴ ②
②
∴t>1 将①代入②得 1<t<4
∴t的范围是(1,4)………………12分
综上t∈(-2,4)
 过(0,0)
过(0,0)则

∴∠OCA=90°, 即
 …………2分
…………2分又∵
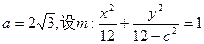
将C点坐标代入得
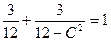
解得 c2=8,b2=4
 ∴椭圆m:
∴椭圆m: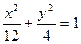 …………4分
…………4分(2)由条件D(0,-2) ∵M(0,t)
1°当k=0时,显然-2<t<2 …………6分
2°当k≠0时,设
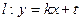
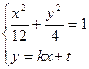 消y得
消y得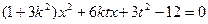 …………8分
…………8分由△>0 可得
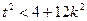 ①………………9分
①………………9分设
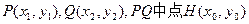
则
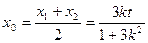
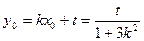
∴
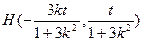 …………11分
…………11分由
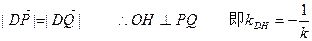
∴
 ②
②∴t>1 将①代入②得 1<t<4
∴t的范围是(1,4)………………12分
综上t∈(-2,4)

练习册系列答案
相关题目
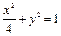 的左、右顶点分别为
的左、右顶点分别为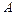 、
、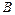 ,曲线
,曲线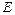 是以椭圆中心为顶点,
是以椭圆中心为顶点,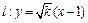 与曲线
与曲线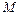 、
、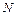 .当
.当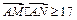 时,求直线
时,求直线 的倾斜角
的倾斜角 的取值范围.
的取值范围.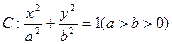 经过点(0,1),离心率
经过点(0,1),离心率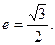
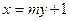 与椭圆C交于A,B两点,点A关于x轴的对称点为A’.试问:当m变化时直线
与椭圆C交于A,B两点,点A关于x轴的对称点为A’.试问:当m变化时直线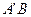 与x轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。
与x轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。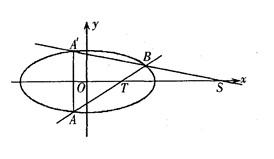
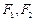 分别是椭圆
分别是椭圆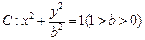 的左、右焦点,过
的左、右焦点,过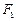 的直线
的直线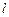 与椭圆
与椭圆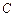 交于A、B两点,且
交于A、B两点,且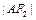 ,
,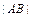 ,
,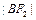 成等差数列.
成等差数列.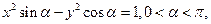 表示焦点在
表示焦点在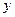 轴上的椭圆,则
轴上的椭圆,则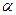 的取值范围是______ _____
的取值范围是______ _____ 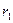 ,
,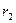 ,则卫星轨道的离心率为 .
,则卫星轨道的离心率为 . 在y轴上的截距为m(m≠0),直线
在y轴上的截距为m(m≠0),直线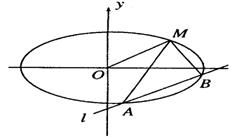
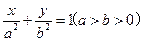 上,AB∥
上,AB∥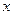 轴,AD过左焦点F,则该椭圆的离心率为 .
轴,AD过左焦点F,则该椭圆的离心率为 .