题目内容
(本小题满分12分)
在一次人才招聘会上,有 三种不同的技工面向社会招聘,已知某技术人员应聘
三种不同的技工面向社会招聘,已知某技术人员应聘 三种技工被录用的概率分别是0.8、0.5、0.2(允许技工人员同时被多种技工录用).
三种技工被录用的概率分别是0.8、0.5、0.2(允许技工人员同时被多种技工录用).
(1)求该技术人员被录用的概率;
(2)设 表示该技术人员被录用的工种数与未被录用的工种数的乘积,求
表示该技术人员被录用的工种数与未被录用的工种数的乘积,求 的分布列和数学期望.
的分布列和数学期望.
在一次人才招聘会上,有
 三种不同的技工面向社会招聘,已知某技术人员应聘
三种不同的技工面向社会招聘,已知某技术人员应聘 三种技工被录用的概率分别是0.8、0.5、0.2(允许技工人员同时被多种技工录用).
三种技工被录用的概率分别是0.8、0.5、0.2(允许技工人员同时被多种技工录用).(1)求该技术人员被录用的概率;
(2)设
 表示该技术人员被录用的工种数与未被录用的工种数的乘积,求
表示该技术人员被录用的工种数与未被录用的工种数的乘积,求 的分布列和数学期望.
的分布列和数学期望.(1)0.92
(2)

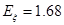
(2)

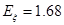
本试题主要是考查了独立事件概率的乘法公式的运用,以及分布列的求解和数学期望值的运用。
(1)因为某技术人员应聘 三种技工被录用的概率分别是0.8、0.5、0.2,因此相互独立,所以该技术人员被录用的概率即为运用对立事件概率的公式得到。
三种技工被录用的概率分别是0.8、0.5、0.2,因此相互独立,所以该技术人员被录用的概率即为运用对立事件概率的公式得到。
(2)由于随机变量 表示该技术人员被录用的工种数与未被录用的工种数的乘积,可知为0,2,然后得到各自的概率值,从而得到分布列和期望值。
表示该技术人员被录用的工种数与未被录用的工种数的乘积,可知为0,2,然后得到各自的概率值,从而得到分布列和期望值。
解:(1)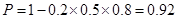 . …………6分
. …………6分
(2)

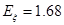 ………………………………………………….12分
………………………………………………….12分
(1)因为某技术人员应聘
 三种技工被录用的概率分别是0.8、0.5、0.2,因此相互独立,所以该技术人员被录用的概率即为运用对立事件概率的公式得到。
三种技工被录用的概率分别是0.8、0.5、0.2,因此相互独立,所以该技术人员被录用的概率即为运用对立事件概率的公式得到。(2)由于随机变量
 表示该技术人员被录用的工种数与未被录用的工种数的乘积,可知为0,2,然后得到各自的概率值,从而得到分布列和期望值。
表示该技术人员被录用的工种数与未被录用的工种数的乘积,可知为0,2,然后得到各自的概率值,从而得到分布列和期望值。解:(1)
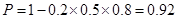 . …………6分
. …………6分(2)

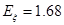 ………………………………………………….12分
………………………………………………….12分
练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 . 当
. 当 . 求
. 求 的
的 ,已知
,已知 时,共有6种坐法.
时,共有6种坐法. ,求
,求 ,假设每次射击是否命中相互之间没有影响.
,假设每次射击是否命中相互之间没有影响.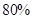 ,二等品率为
,二等品率为 ;乙产品的一等品率为
;乙产品的一等品率为 ,二等品率为
,二等品率为 .生产
.生产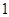 件甲产品,若是一等品,则获利
件甲产品,若是一等品,则获利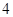 万元,若是二等品,则亏损
万元,若是二等品,则亏损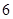 万元,若是二等品,则亏损
万元,若是二等品,则亏损 万
万 (单位:万元),求
(单位:万元),求 万元的概率.
万元的概率. ,乙队中三人答对的概率分别为
,乙队中三人答对的概率分别为 ,且各人回答得正确与否相互之间没有影响.
,且各人回答得正确与否相互之间没有影响. 表示甲队的总得分,求随机变量
表示甲队的总得分,求随机变量 表示事件“甲、乙两队总得分之和为
表示事件“甲、乙两队总得分之和为 ”,用
”,用 表示事件“甲队总得分大于乙队总得分”,求
表示事件“甲队总得分大于乙队总得分”,求 .
.
 为获得k(k=1,2,3)等奖的折扣率,求随机变量
为获得k(k=1,2,3)等奖的折扣率,求随机变量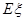 ;(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量
;(II)若有3人次(投入l球为l人次)参加促销活动,记随机变量 为获得1等奖或2等奖的人次,求
为获得1等奖或2等奖的人次,求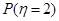 .
.