题目内容
(12分) 一盒中装有分别标记着1,2,3,4的4个小球,每次从袋中取出一只球,设每只小球被取出的可能性相同.
(1)若每次取出的球不放回盒中,现连续取三次球,求恰好第三次取出的球的标号为最大数字的球的概率;
(2)若每次取出的球放回盒中,然后再取出一只球,现连续取三次球,这三次取出的球中标号最大数字为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
(1)若每次取出的球不放回盒中,现连续取三次球,求恰好第三次取出的球的标号为最大数字的球的概率;
(2)若每次取出的球放回盒中,然后再取出一只球,现连续取三次球,这三次取出的球中标号最大数字为
 ,求
,求 的分布列与数学期望.
的分布列与数学期望. (1)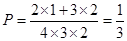 ;
;
(2)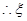 的分布列为
的分布列为
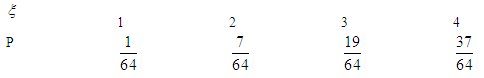
所以,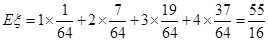
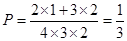 ;
; (2)
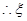 的分布列为
的分布列为 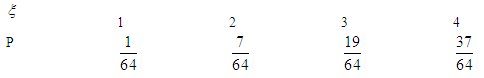
所以,
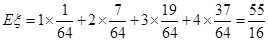
本题考查概率的性质和应用、离散型随机变量及其分布列,解题时要认真审题,仔细解答,注意离散型随机变量概率分布列的求法,属于中档题.
(1)四个球中取三个,由于小球编号不同,故取法共有A43,若第三次取出的标号为最大数字,此数字可能是3或4,分别求出符合题意的种数即可;
(2)ξ的取值为1、2、3、4,然后根据 P(ξ=k)=(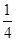 )3+C 23 (
)3+C 23 (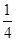 )2(k-
)2(k-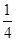 )+3 (
)+3 (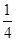 )(k-
)(k- 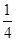 )2求出相应的概率,列出分布列,最后利用数学期望公式进行求解即可
)2求出相应的概率,列出分布列,最后利用数学期望公式进行求解即可
解:(1)当恰好第三次取出的球的标号为最大数字时,则第三次取出的球可能是3或4
得: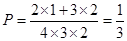
(2) 的可能取值为1,2,3,4
的可能取值为1,2,3,4
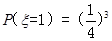
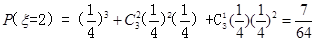
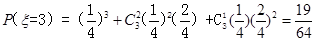
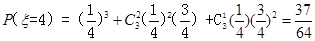
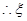 的分布列为
的分布列为
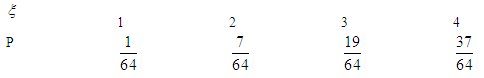
所以,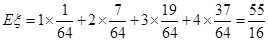
(1)四个球中取三个,由于小球编号不同,故取法共有A43,若第三次取出的标号为最大数字,此数字可能是3或4,分别求出符合题意的种数即可;
(2)ξ的取值为1、2、3、4,然后根据 P(ξ=k)=(
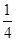 )3+C 23 (
)3+C 23 (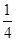 )2(k-
)2(k-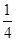 )+3 (
)+3 (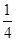 )(k-
)(k- 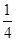 )2求出相应的概率,列出分布列,最后利用数学期望公式进行求解即可
)2求出相应的概率,列出分布列,最后利用数学期望公式进行求解即可解:(1)当恰好第三次取出的球的标号为最大数字时,则第三次取出的球可能是3或4
得:
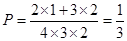
(2)
 的可能取值为1,2,3,4
的可能取值为1,2,3,4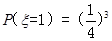
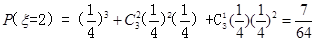
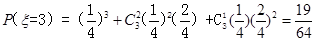
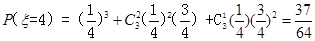
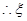 的分布列为
的分布列为 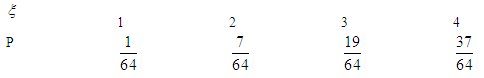
所以,
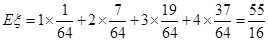

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 服从的分布列如图,则随机变量
服从的分布列如图,则随机变量 等于 ( )
等于 ( )




 B.
B. C.
C.  D.
D. 

 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求: 的概率分布和数学期望;
的概率分布和数学期望; )=
)= ,则P(Y
,则P(Y 三种不同的技工面向社会招聘,已知某技术人员应聘
三种不同的技工面向社会招聘,已知某技术人员应聘 表示该技术人员被录用的工种数与未被录用的工种数的乘积,求
表示该技术人员被录用的工种数与未被录用的工种数的乘积,求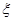 .
. ,一等品率提高为
,一等品率提高为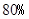 .如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少? 四条旅游线路,每个旅游团可任选其中一条线路,则选择
四条旅游线路,每个旅游团可任选其中一条线路,则选择 线路旅游团数
线路旅游团数 的数学期望
的数学期望 ;
;  满足
满足 ,
, ,则
,则 等于( )
等于( )