题目内容
(本题满分10分)在1,2,3…,9,这9个自然数中,任取3个数.
(Ⅰ)求这3个数中,恰有一个是偶数的概率;
(Ⅱ)记X为这三个数中两数相邻的组数,(例如:若取出的数1、2、3,则有两组相邻的数1、2和2、3,此时X的值是2)。求随机变量X的分布列及其数学期望EX.
(Ⅰ)求这3个数中,恰有一个是偶数的概率;
(Ⅱ)记X为这三个数中两数相邻的组数,(例如:若取出的数1、2、3,则有两组相邻的数1、2和2、3,此时X的值是2)。求随机变量X的分布列及其数学期望EX.
(I) ;
;
(II)随机变量X的取值为 的分布列为
的分布列为
所以 的数学期望为
的数学期望为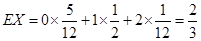
 ;
;(II)随机变量X的取值为
 的分布列为
的分布列为| X | 0 | 1 | 2 |
| P | 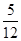 |  |  |
 的数学期望为
的数学期望为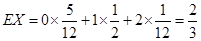
本试题主要是考查了古典概型概率的计算,以及分布列的求解和数学期望值的综合运用。
(1)这3个数恰有一个是偶数”为事件A,则
(2)因为随机变量X的取值为 ,则各个取值的概率利用概率公式求解得到,从而得到分布列和数学期望值。
,则各个取值的概率利用概率公式求解得到,从而得到分布列和数学期望值。
解析:(I)记“这3个数恰有一个是偶数”为事件A,则 ;
;
(II)随机变量X的取值为 的分布列为
的分布列为
所以 的数学期望为
的数学期望为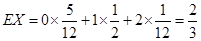
(1)这3个数恰有一个是偶数”为事件A,则

(2)因为随机变量X的取值为
 ,则各个取值的概率利用概率公式求解得到,从而得到分布列和数学期望值。
,则各个取值的概率利用概率公式求解得到,从而得到分布列和数学期望值。解析:(I)记“这3个数恰有一个是偶数”为事件A,则
 ;
;(II)随机变量X的取值为
 的分布列为
的分布列为| X | 0 | 1 | 2 |
| P | 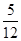 |  |  |
 的数学期望为
的数学期望为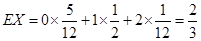

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
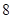 个等级,等级系数
个等级,等级系数 依次为
依次为 ,其中
,其中 为标准
为标准 ,
, 为标准
为标准 ,产品的等级系数越大表明产品的质量越好,已知某厂执行标准
,产品的等级系数越大表明产品的质量越好,已知某厂执行标准 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下: 的为一等品,等级系数
的为一等品,等级系数 的为二等品,等级系数
的为二等品,等级系数 的为三等品,
的为三等品, ,从该厂生产的产品中任取一件,其利润记为
,从该厂生产的产品中任取一件,其利润记为 ,用这个样本的频率分布估计总体分布,将频率视为概率,求
,用这个样本的频率分布估计总体分布,将频率视为概率,求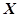 ~
~ ,且
,且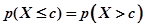 ,则
,则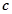 的值( )
的值( )
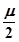
 三种不同的技工面向社会招聘,已知某技术人员应聘
三种不同的技工面向社会招聘,已知某技术人员应聘 表示该技术人员被录用的工种数与未被录用的工种数的乘积,求
表示该技术人员被录用的工种数与未被录用的工种数的乘积,求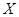 ,求
,求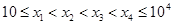 ,
,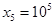 . 随机变量
. 随机变量 取值
取值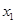 、
、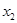 、
、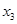 、
、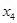 、
、 的概率均为0.2,随机变量
的概率均为0.2,随机变量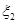 取值
取值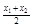 、
、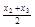 、
、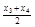 、
、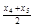 、
、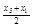 的概率也为0.2.
的概率也为0.2. 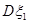 、
、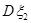 分别为
分别为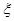 满足
满足 ,
, ,则
,则 等于( )
等于( )