题目内容
甲同学在军训中,练习射击项目,他射击命中目标的概率是 ,假设每次射击是否命中相互之间没有影响.
,假设每次射击是否命中相互之间没有影响.
(Ⅰ)在3次射击中,求甲至少有1次命中目标的概率;
(Ⅱ)在射击中,若甲命中目标,则停止射击,否则继续射击,直至命中目标,但射击次数最多不超过3次,求甲射击次数的分布列和数学期望.
 ,假设每次射击是否命中相互之间没有影响.
,假设每次射击是否命中相互之间没有影响.(Ⅰ)在3次射击中,求甲至少有1次命中目标的概率;
(Ⅱ)在射击中,若甲命中目标,则停止射击,否则继续射击,直至命中目标,但射击次数最多不超过3次,求甲射击次数的分布列和数学期望.
(Ⅰ)解:记“在3次射击中,甲至少有1次命中目标”为事件A。 1分
则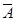 表示事件“在3次射击中,甲没有命中目标。” 2分
表示事件“在3次射击中,甲没有命中目标。” 2分
故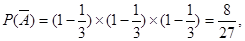 4分
4分
所以 。 6分
。 6分
(Ⅱ)解:记甲的射击次数为X,则X的可能取值为1,2,3 7分
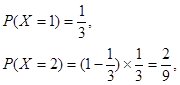
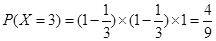 10分
10分
X的分布列为:
11分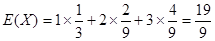 (环)。 13分
(环)。 13分
则
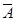 表示事件“在3次射击中,甲没有命中目标。” 2分
表示事件“在3次射击中,甲没有命中目标。” 2分故
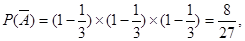 4分
4分所以
 。 6分
。 6分 (Ⅱ)解:记甲的射击次数为X,则X的可能取值为1,2,3 7分
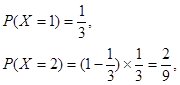
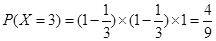 10分
10分X的分布列为:
| X | 1 | 2 | 3 |
| P | 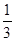 | 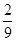 | 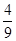 |
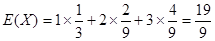 (环)。 13分
(环)。 13分本试题朱亚奥是考查了独立重复试验中事件发生的概率的运用。以及二项分布的概率的运用。
(1)因为射击命中目标的概率是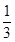 ,假设每次射击是否命中相互之间没有影响.
,假设每次射击是否命中相互之间没有影响.
则在3次射击中,求甲至少有1次命中目标的概率可以根据对立事件的概率求解得到。
(2)那么先分析随机变量各个取值的情况,得到各个取值的概率值得到求解。
(1)因为射击命中目标的概率是
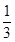 ,假设每次射击是否命中相互之间没有影响.
,假设每次射击是否命中相互之间没有影响.则在3次射击中,求甲至少有1次命中目标的概率可以根据对立事件的概率求解得到。
(2)那么先分析随机变量各个取值的情况,得到各个取值的概率值得到求解。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为取出3球中白球的个数,已知
为取出3球中白球的个数,已知 .
. 的分布列及其数学期望.
的分布列及其数学期望. )=
)= ,则P(Y
,则P(Y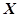 ~
~ ,且
,且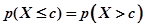 ,则
,则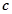 的值( )
的值( )
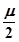
 三种不同的技工面向社会招聘,已知某技术人员应聘
三种不同的技工面向社会招聘,已知某技术人员应聘 表示该技术人员被录用的工种数与未被录用的工种数的乘积,求
表示该技术人员被录用的工种数与未被录用的工种数的乘积,求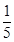
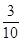
 四条旅游线路,每个旅游团可任选其中一条线路,则选择
四条旅游线路,每个旅游团可任选其中一条线路,则选择 线路旅游团数
线路旅游团数 的数学期望
的数学期望 ;
; 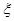 满足
满足 ,
, ,则
,则 等于( )
等于( )