题目内容
甲乙两队参加奥运知识竞赛,每队三人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为 ,乙队中三人答对的概率分别为
,乙队中三人答对的概率分别为 ,且各人回答得正确与否相互之间没有影响.
,且各人回答得正确与否相互之间没有影响.
(1)若用 表示甲队的总得分,求随机变量
表示甲队的总得分,求随机变量 分布列和数学期望;
分布列和数学期望;
(2)用 表示事件“甲、乙两队总得分之和为
表示事件“甲、乙两队总得分之和为 ”,用
”,用 表示事件“甲队总得分大于乙队总得分”,求
表示事件“甲队总得分大于乙队总得分”,求 .
.
 ,乙队中三人答对的概率分别为
,乙队中三人答对的概率分别为 ,且各人回答得正确与否相互之间没有影响.
,且各人回答得正确与否相互之间没有影响.(1)若用
 表示甲队的总得分,求随机变量
表示甲队的总得分,求随机变量 分布列和数学期望;
分布列和数学期望;(2)用
 表示事件“甲、乙两队总得分之和为
表示事件“甲、乙两队总得分之和为 ”,用
”,用 表示事件“甲队总得分大于乙队总得分”,求
表示事件“甲队总得分大于乙队总得分”,求 .
.解:(1)
所以
 的分布列为
的分布列为 |  |  | 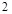 [ [ |  |
 | 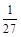 |  |  | 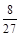 |
 的数学期望
的数学期望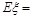

(2)
 .
.本试题主要是考查了分布列的求解和数学期望值的运算,统统是利用了独立事件的概率的乘法公式,和n次独立重复试验中事件发生k次的概率公式表示得到结论。
(1)利用已知条件,分析得到, 的可能取值为
的可能取值为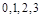 ,然后利用独立重复试验中概率的公式求解得到各个概率值。进而得到分布列
,然后利用独立重复试验中概率的公式求解得到各个概率值。进而得到分布列
(2)由于事件A,B相互独立,则利用各种情况,分析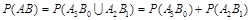 ,结合乘法公式得到结论。
,结合乘法公式得到结论。
解:(1)由题意知, 的可能取值为
的可能取值为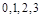 ,则有
,则有
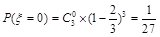 ,
, ,
,
 ,
, .
.
所以 的分布列为
的分布列为
故 的数学期望
的数学期望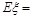

(2)用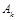 表示事件“甲队得
表示事件“甲队得 分”,用
分”,用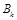 表示事件“乙队得
表示事件“乙队得 分”.因
分”.因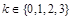 ,且由于
,且由于 与
与 为互斥事件,故
为互斥事件,故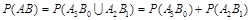 .
.
∴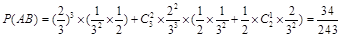 .
.
(1)利用已知条件,分析得到,
 的可能取值为
的可能取值为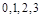 ,然后利用独立重复试验中概率的公式求解得到各个概率值。进而得到分布列
,然后利用独立重复试验中概率的公式求解得到各个概率值。进而得到分布列(2)由于事件A,B相互独立,则利用各种情况,分析
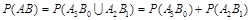 ,结合乘法公式得到结论。
,结合乘法公式得到结论。解:(1)由题意知,
 的可能取值为
的可能取值为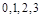 ,则有
,则有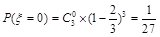 ,
, ,
, ,
, .
.所以
 的分布列为
的分布列为 |  |  | 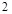 [ [ |  |
 | 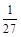 |  |  | 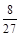 |
 的数学期望
的数学期望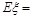

(2)用
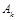 表示事件“甲队得
表示事件“甲队得 分”,用
分”,用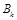 表示事件“乙队得
表示事件“乙队得 分”.因
分”.因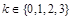 ,且由于
,且由于 与
与 为互斥事件,故
为互斥事件,故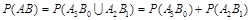 .
.∴
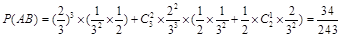 .
.
练习册系列答案
相关题目
 三种不同的技工面向社会招聘,已知某技术人员应聘
三种不同的技工面向社会招聘,已知某技术人员应聘 表示该技术人员被录用的工种数与未被录用的工种数的乘积,求
表示该技术人员被录用的工种数与未被录用的工种数的乘积,求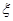 ,求随机变量
,求随机变量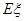 .(8分)
.(8分)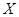 ,求
,求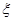 .
. ,一等品率提高为
,一等品率提高为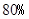 .如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?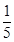
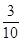
 .
. ,试写出
,试写出 四条旅游线路,每个旅游团可任选其中一条线路,则选择
四条旅游线路,每个旅游团可任选其中一条线路,则选择 线路旅游团数
线路旅游团数 的数学期望
的数学期望 ;
;