题目内容
口袋里装有7个大小相同小球, 其中三个标有数字1, 两个标有数字2, 一个标有数字3, 一个标有数字4.
(Ⅰ) 第一次从口袋里任意取一球, 放回口袋里后第二次再任意取一球, 记第一次与第二次取到小球上的数字之和为 . 当
. 当 为何值时, 其发生的概率最大? 说明理由;
为何值时, 其发生的概率最大? 说明理由;
(Ⅱ) 第一次从口袋里任意取一球, 不再放回口袋里, 第二次再任意取一球, 记第一次与第二次取到小球上的数字之和为 . 求
. 求 的分布列和数学期望.
的分布列和数学期望.
(Ⅰ) 第一次从口袋里任意取一球, 放回口袋里后第二次再任意取一球, 记第一次与第二次取到小球上的数字之和为
 . 当
. 当 为何值时, 其发生的概率最大? 说明理由;
为何值时, 其发生的概率最大? 说明理由; (Ⅱ) 第一次从口袋里任意取一球, 不再放回口袋里, 第二次再任意取一球, 记第一次与第二次取到小球上的数字之和为
 . 求
. 求 的分布列和数学期望.
的分布列和数学期望.见解析
本试题主要是考查了古典概型概率的运算以及随机变量的分布列的求解和数学期望值的运算的 综合运用。
(1)因为第一次从口袋里任意取一球, 放回口袋里后第二次再任意取一球, 记第一次与第二次取到小球上的数字之和为 .利用独立事件的概率公式求解得到
.利用独立事件的概率公式求解得到
(2)第一次从口袋里任意取一球, 不再放回口袋里, 第二次再任意取一球, 记第一次与第二次取到小球上的数字之和为 .因为是不放回的抽取,因此运用古典概型概率求解概率值,得到结论。
.因为是不放回的抽取,因此运用古典概型概率求解概率值,得到结论。
解:(Ⅰ) 可能的取值为
可能的取值为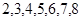
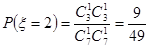
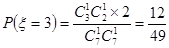
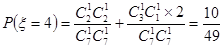
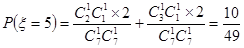
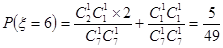
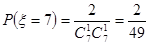
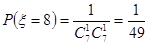
(Ⅱ) 可能的取值为
可能的取值为
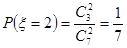
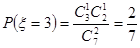
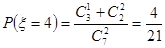
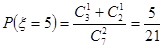
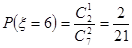
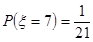
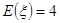
(1)因为第一次从口袋里任意取一球, 放回口袋里后第二次再任意取一球, 记第一次与第二次取到小球上的数字之和为
 .利用独立事件的概率公式求解得到
.利用独立事件的概率公式求解得到(2)第一次从口袋里任意取一球, 不再放回口袋里, 第二次再任意取一球, 记第一次与第二次取到小球上的数字之和为
 .因为是不放回的抽取,因此运用古典概型概率求解概率值,得到结论。
.因为是不放回的抽取,因此运用古典概型概率求解概率值,得到结论。解:(Ⅰ)
 可能的取值为
可能的取值为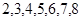
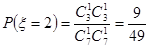
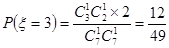
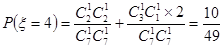
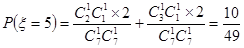
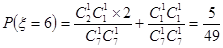
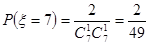
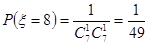
(Ⅱ)
 可能的取值为
可能的取值为
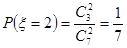
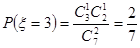
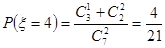
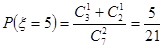
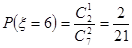
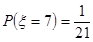
 | 2 | 3 | 4 | 5 | 6 | 7 |
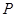 | 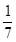 | 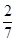 | 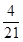 | 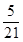 | 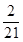 | 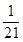 |
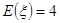

练习册系列答案
相关题目
 ,遇到红灯时停留的时间都是2min.
,遇到红灯时停留的时间都是2min. 的分布列及期望.
的分布列及期望. 的分布列和数学期望;
的分布列和数学期望; 表示取出的3个小球上的最大数字,求:
表示取出的3个小球上的最大数字,求: 的概率分布和数学期望;
的概率分布和数学期望; )=
)= ,则P(Y
,则P(Y 三种不同的技工面向社会招聘,已知某技术人员应聘
三种不同的技工面向社会招聘,已知某技术人员应聘 表示该技术人员被录用的工种数与未被录用的工种数的乘积,求
表示该技术人员被录用的工种数与未被录用的工种数的乘积,求 ,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.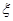 ,求随机变量
,求随机变量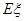 .(8分)
.(8分)