题目内容
14. 已知点p(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为1的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M.
已知点p(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为1的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M.(Ⅰ) 求椭圆Γ的离心率e;
(Ⅱ) 试判断直线PA,PM,PB的斜率是否成等差数列?若成等差数列,给出证明;若不成等差数列,请说明理由.
分析 (Ⅰ)把点P的坐标代入椭圆方程,结合隐含条件化为关于e的方程,则椭圆的离心率可求;
(Ⅱ)由(Ⅰ)中求出的椭圆的离心率,把a,b用含有c的代数式表示,求出直线m的方程,和椭圆方程联立,利用根与系数的关系得到k1+k3,并求得k2的值,由k1+k3=k2说明直线PA,PM,PB的斜率成等差数列.
解答 解:(Ⅰ)∵点p(c,$\frac{3}{2}$c)在椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1上,
∴$\frac{{c}^{2}}{{a}^{2}}+\frac{9{c}^{2}}{4{b}^{2}}=1$.
整理得,4a4-17a2c2+4c4=0,即4e4-17e2+4=0,
解得$e=\frac{1}{2}$或e=2 (舍),
∴离心率$e=\frac{1}{2}$;
(Ⅱ)直线PA,PM,PB的斜率成等差数列,证明如下:
由(Ⅰ)知,$a=2c,b=\sqrt{3}c$,∴椭圆E:3x2+4y2=12c2,
直线m的方程为y=x-c.
代入椭圆方程并整理,得7x2-8cx-8c2=0.
设A(x1,y1),B(x2,y2),直线PA,PM,PB的斜率分别为k1,k2,k3,
则有${x}_{1}+{x}_{2}=\frac{8c}{7},{x}_{1}•{x}_{2}=-\frac{8{c}^{2}}{7}$.
可知M的坐标为(4c,3c).
∴${k}_{1}+{k}_{3}=\frac{{y}_{1}-\frac{3}{2}c}{{x}_{1}-c}+\frac{{y}_{2}-\frac{3}{2}c}{{x}_{2}-c}$=$\frac{2{x}_{1}{x}_{2}-\frac{7}{2}c({x}_{1}+{x}_{2})+5{c}^{2}}{{x}_{1}{x}_{2}-c({x}_{1}+{x}_{2})+{c}^{2}}=1$,
$2{k}_{2}=\frac{2(\frac{3}{2}c-3c)}{c-4c}=1$,
∴k1+k3=2k2.
故直线PA,PM,PB的斜率成等差数列.
点评 本题主要考查了直线与椭圆的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系解题,是处理这类问题的最为常用的方法,但圆锥曲线的特点是计算量比较大,要求考试具备较强的运算推理的能力,该题是中档题.

| A. | 1 | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
 如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=$\sqrt{3}a$,E为BC中点.
如图,四边形ABCD为梯形,AB∥CD,PD⊥平面ABCD,∠BAD=∠ADC=90°,DC=2AB=2a,DA=$\sqrt{3}a$,E为BC中点.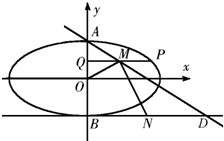 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率是$\frac{{\sqrt{3}}}{2}$,A,B分别是C的上下顶点,点B在直线l:y=-1上.