题目内容
13. 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)过点(0,-2),且离心率为$\frac{{\sqrt{5}}}{3}$.(1)求椭圆E的方程;
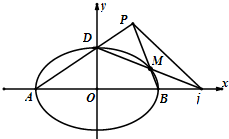
(2)如图,ABD是椭圆E的顶点,M是椭圆E上除顶点外的任意一点,直线DM交x轴于点Q,直线AD交BM于点P,设BM的斜率为k,PQ的斜率为m,求动点N(m,k)轨迹方程.
分析 (1)由已知得b和$\frac{c}{a}$,结合隐含条件a2=b2+c2求得a,b的值,则椭圆方程可求;
(2)由题意求出A,B,D的坐标,得到直线AD的方程,再设出直线BP方程,联立两直线方程求得P的坐标,联立直线BP的方程与椭圆方程求得M的坐标,再由M,D,Q三点共线求得Q的坐标,代入两点求斜率公式得到直线PQ的斜率,整理后即可得到关于k,m的等式,则可求得点N(m,k)的轨迹方程.
解答 解:(1)依题意,b=2,$\frac{c}{a}$=$\frac{\sqrt{5}}{3}$,又a2=b2+c2,
∴5a2=9c2=9(a2-b2)=9a2-36,即a2=9.
∴椭圆E的方程为:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1;
(2)由(1)知,A(-3,0),B(3,0),D(0,2),
∴直线AD的方程为y=$\frac{2}{3}$x+2,
由题意,直线BP的方程为y=k(x-3),k≠0且k$≠±\frac{2}{3}$,
由$\left\{\begin{array}{l}{y=\frac{2}{3}x+2}\\{y=k(x-3)}\end{array}\right.$,解得P($\frac{9k+6}{3k-2}$,$\frac{12k}{3k-2}$),
设M(x1,y1),则由$\left\{\begin{array}{l}{y=k(x-3)}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,
消去y整理得(9k2+4)x2-54k2x+81k2-36=0.
∴3x1=$\frac{81{k}^{2}-36}{4+9{k}^{2}}$,即x1=$\frac{27{k}^{2}-12}{4+9{k}^{2}}$,
即M($\frac{27{k}^{2}-12}{4+9{k}^{2}}$,-$\frac{24k}{4+9{k}^{2}}$),
设Q(x2,0),则由M,D,Q三点共线得:kDM=kDQ,
即$\frac{\frac{-24k}{4+9{k}^{2}}-2}{\frac{27{k}^{2}-12}{4+9{k}^{2}}}$=$\frac{-2}{{x}_{2}}$,∴x2=$\frac{9k-6}{3k+2}$,则Q($\frac{9k-6}{3k+2}$,0),
∴PQ的斜率m=$\frac{\frac{12k}{3k-2}-0}{\frac{9k+6}{3k-2}-\frac{9k-6}{3k+2}}$=$\frac{3k+2}{6}$.
∴3k+2=6m,即点N(m,k)的轨迹方程为6x-3y-2=0.
点评 本题考查了椭圆方程的求法,考查了椭圆的简单性质,训练了直线和圆锥曲线位置关系的应用,(2)的求解着重体现了“设而不求”和整体运算思想方法,属中档题.

 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°AB=PC=2,AP=BP=$\sqrt{2}$
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°AB=PC=2,AP=BP=$\sqrt{2}$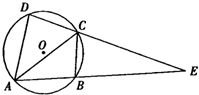 如图所示,四边形ABCD的外接圆为圆O,线段AB与线段DC的延长线交于点E,$\frac{AD}{DE}$=$\frac{1}{3}$.
如图所示,四边形ABCD的外接圆为圆O,线段AB与线段DC的延长线交于点E,$\frac{AD}{DE}$=$\frac{1}{3}$.