题目内容
15. 如图在以OA为半径的半圆M中,有三个半径为1的相同的半圆,在半圆M中任取一点N.
如图在以OA为半径的半圆M中,有三个半径为1的相同的半圆,在半圆M中任取一点N.(1)求点N位于区域E的概率;
(2)求点N位于区域F的概率.
分析 由题意求出区域E、F及半圆M的面积.
(1)由区域E的面积除以半圆M的面积得答案;
(2)由区域F的面积除以半圆M的面积得答案.
解答 解:如图,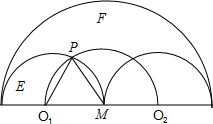
以MO1P为圆心角的扇形的面积为$\frac{1}{2}×\frac{π}{3}×1×1=\frac{π}{6}$,
等边三角形O1MP的面积为$\frac{1}{2}×1×\frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}$.
∴以MO1P为圆心角的小弓形的面积为$\frac{π}{6}-\frac{\sqrt{3}}{4}$.
∴区域E的面积为$\frac{π}{2}-\frac{π}{6}-\frac{π}{6}+\frac{\sqrt{3}}{4}=\frac{π}{6}+\frac{\sqrt{3}}{4}$.
区域F的面积为2π$-\frac{π}{2}-\frac{π}{2}$$-\frac{π}{6}+2(\frac{π}{6}-\frac{\sqrt{3}}{4})$=$\frac{7π}{6}-\frac{\sqrt{3}}{2}$.
半圆M的面积为2π.
(1)点N位于区域E的概率为$\frac{\frac{π}{6}+\frac{\sqrt{3}}{4}}{2π}=\frac{1}{12}+\frac{\sqrt{3}}{8π}$;
(2)点N位于区域F的概率为$\frac{\frac{7π}{6}-\frac{\sqrt{3}}{2}}{2π}=\frac{7}{12}-\frac{\sqrt{3}}{4π}$.
点评 本题考查了几何概型,考查了扇形面积公式的应用,是中低档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°AB=PC=2,AP=BP=$\sqrt{2}$
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°AB=PC=2,AP=BP=$\sqrt{2}$