题目内容
17.已知定长为3的线段AB的端点在抛物线y2=2x上移动,M为AB的中点,求M到y轴的最短距离.分析 先设出A,B的坐标,根据抛物线方程可求得其准线方程,进而可表示出M到y轴距离,根据抛物线的定义结合两边之和大于第三边且A,B,F三点共线时取等号判断出$\frac{|AF|+|BF|}{2}$的最小值.
解答 解:设A(x1,y1),B(x2,y2),
由抛物线方程y2=2x,得抛物线准线x=-$\frac{1}{2}$,
∴所求的距离为:
d=|$\frac{{x}_{1}+{x}_{2}}{2}$|=$\frac{{x}_{1}+{x}_{2}}{2}=\frac{{x}_{1}+\frac{1}{2}+{x}_{2}+\frac{1}{2}}{2}-\frac{1}{2}$
=$\frac{|AF|+|BF|}{2}$$-\frac{1}{2}$≥$\frac{|AB|}{2}-\frac{1}{2}$=$\frac{3}{2}-\frac{1}{2}$=1.
点评 本题主要考查抛物线的简单性质、利用不等式求最值等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想,属于中档题.

练习册系列答案
相关题目
10.已知函数f(x)=$\left\{\begin{array}{l}{1-|1-x|,x∈(-∞,2)}\\{2f(x-2),x∈[2,+∞)}\end{array}\right.$,设方程f(x)=2${\;}^{\frac{x-1}{2}}$的根从小到大依次为x1,x2,…xn,…,n∈N*,则数列{f(xn)}的前n项和为( )
| A. | n2 | B. | n2+n | C. | 2n-1 | D. | 2n+1-1 |
6.在边长为1的正三角形ABC中,|$\overrightarrow{AB}$-$\overrightarrow{BC}$|的值为( )
| A. | 1 | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
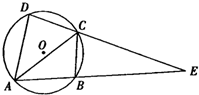 如图所示,四边形ABCD的外接圆为圆O,线段AB与线段DC的延长线交于点E,$\frac{AD}{DE}$=$\frac{1}{3}$.
如图所示,四边形ABCD的外接圆为圆O,线段AB与线段DC的延长线交于点E,$\frac{AD}{DE}$=$\frac{1}{3}$.