题目内容
13.若a,b是函数f(x)=x2-px+q(p>0,q>0)的两个不同的零点,且a,b,-2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p+q的值等于9.分析 由一元二次方程根与系数的关系得到a+b=p,ab=q,再由a,b,-2这三个数可适当排序后成等差数列,也可适当排序后成等比数列列关于a,b的方程组,求得a,b后得答案.
解答 解:由题意可得:a+b=p,ab=q,
∵p>0,q>0,
可得a>0,b>0,
又a,b,-2这三个数可适当排序后成等差数列,也可适当排序后成等比数列,
可得$\left\{\begin{array}{l}{2b=a-2}\\{ab=4}\end{array}\right.$①或$\left\{\begin{array}{l}{2a=b-2}\\{ab=4}\end{array}\right.$②.
解①得:$\left\{\begin{array}{l}{a=4}\\{b=1}\end{array}\right.$;解②得:$\left\{\begin{array}{l}{a=1}\\{b=4}\end{array}\right.$.
∴p=a+b=5,q=1×4=4,
则p+q=9.
故答案为:9.
点评 本题考查了一元二次方程根与系数的关系,考查了等差数列和等比数列的性质,是基础题.

练习册系列答案
相关题目
1.下列函数为奇函数的是( )
| A. | y=$\sqrt{x}$ | B. | y=ex | C. | y=cosx | D. | y=ex-e-x |
8.变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≥0}\\{x-2y+2≥0}\\{mx-y≤0}\end{array}\right.$,若z=2x-y的最大值为2,则实数m等于( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
5.阅读如图所示的程序框图,运行相应的程序,则输出的结果为( )
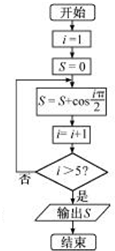

| A. | 2 | B. | 1 | C. | 0 | D. | -1 |