题目内容
3．已知$\overrightarrow{e}$1，$\overrightarrow{e}$2是平面单位向量，且$\overrightarrow{e}$1•$\overrightarrow{e}$2=$\frac{1}{2}$，若平面向量$\overrightarrow{b}$满足$\overrightarrow{b}$•$\overrightarrow{e}$1=$\overrightarrow{b}$•$\overrightarrow{{e}_{2}}$=1，则|$\overrightarrow{b}$|=$\frac{2\sqrt{3}}{3}$．分析 根据数量积得出$\overrightarrow{e}$1，$\overrightarrow{e}$2夹角为60°，＜$\overrightarrow{b}$，$\overrightarrow{e}$1＞=＜$\overrightarrow{b}$，$\overrightarrow{e}$2＞=30°，运用数量积的定义判断求解即可．
解答 解：∵$\overrightarrow{e}$1，$\overrightarrow{e}$2是平面单位向量，且$\overrightarrow{e}$1•$\overrightarrow{e}$2=$\frac{1}{2}$，
∴$\overrightarrow{e}$1，$\overrightarrow{e}$2夹角为60°，
∵向量$\overrightarrow{b}$满足$\overrightarrow{b}$•$\overrightarrow{e}$1=$\overrightarrow{b}$•$\overrightarrow{{e}_{2}}$=1
∴$\overrightarrow{b}$与$\overrightarrow{e}$1，$\overrightarrow{e}$2夹角相等，且为锐角，
∴$\overrightarrow{b}$应该在$\overrightarrow{e}$1，$\overrightarrow{e}$2夹角的平分线上，
即＜$\overrightarrow{b}$，$\overrightarrow{e}$1＞=＜$\overrightarrow{b}$，$\overrightarrow{e}$2＞=30°，
|$\overrightarrow{b}$|×1×cos30°=1，
∴|$\overrightarrow{b}$|=$\frac{2\sqrt{3}}{3}$
故答案为：$\frac{2\sqrt{3}}{3}$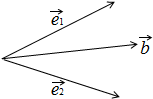
点评 本题简单的考查了平面向量的运算，数量积的定义，几何图形的运用，属于容易题，关键是判断夹角即可．
阅读快车系列答案| W | 12 | 15 | 18 |
| P | 0.3 | 0.5 | 0.2 |
（1）求Z的分布列和均值；
（2）若每天可获取的鲜牛奶数量相互独立，求3天中至少有1天的最大获利超过10000元的概率．
| A． | 若t确定，则b2唯一确定 | B． | 若t确定，则a2+2a唯一确定 | ||
| C． | 若t确定，则sin$\frac{b}{2}$唯一确定 | D． | 若t确定，则a2+a唯一确定 |
如图，已知抛物线C1：y=$\frac{1}{4}$x2，圆C2：x2+（y-1）2=1，过点P（t，0）（t＞0）作不过原点O的直线PA，PB分别与抛物线C1和圆C2相切，A，B为切点．