题目内容
8.变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≥0}\\{x-2y+2≥0}\\{mx-y≤0}\end{array}\right.$,若z=2x-y的最大值为2,则实数m等于( )| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数求得m的值.
解答 解:由约束条件$\left\{\begin{array}{l}{x+y≥0}\\{x-2y+2≥0}\\{mx-y≤0}\end{array}\right.$作出可行域如图,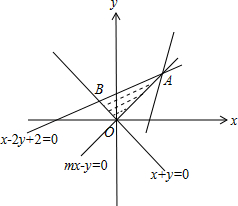
联立$\left\{\begin{array}{l}{x-2y+2=0}\\{mx-y=0}\end{array}\right.$,解得A($\frac{2}{2m-1},\frac{2m}{2m-1}$),
化目标函数z=2x-y为y=2x-z,
由图可知,当直线过A时,直线在y轴上的截距最小,z有最大值为$\frac{4}{2m-1}-\frac{2m}{2m-1}=\frac{4-2m}{2m-1}=2$,
解得:m=1.
故选:C.
点评 本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
18.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{1}{3}+π$ | B. | $\frac{2}{3}+π$ | C. | $\frac{1}{3}+2π$ | D. | $\frac{2}{3}+2π$ |
19.设实数x,y满足$\left\{\begin{array}{l}2x+y≤10\\ x+2y≤14\\ x+y≥6\end{array}\right.$,则xy的最大值为( )
| A. | $\frac{25}{2}$ | B. | $\frac{49}{2}$ | C. | 12 | D. | 16 |
16.随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
(Ⅰ)在4月份任取一天,估计西安市在该天不下雨的概率;
(Ⅱ)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
(Ⅰ)在4月份任取一天,估计西安市在该天不下雨的概率;
(Ⅱ)西安市某学校拟从4月份的一个晴天开始举行连续2天的运动会,估计运动会期间不下雨的概率.
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
| 日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
20.若集合A={i,i2,i3,i4}(i是虚数单位),B={1,-1},则A∩B等于( )
| A. | {-1} | B. | {1} | C. | {1,-1} | D. | ∅ |
18.设实数a,b,t满足|a+1|=|sinb|=t.则( )
| A. | 若t确定,则b2唯一确定 | B. | 若t确定,则a2+2a唯一确定 | ||
| C. | 若t确定,则sin$\frac{b}{2}$唯一确定 | D. | 若t确定,则a2+a唯一确定 |
 已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)过点$(0,\sqrt{2})$,且离心率e为$\frac{{\sqrt{2}}}{2}$.
已知椭圆E:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)过点$(0,\sqrt{2})$,且离心率e为$\frac{{\sqrt{2}}}{2}$.