Question

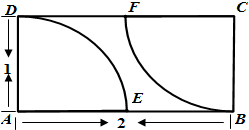
如图，在矩形区域ABCD的A，C两点处各有一个通信基站，假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF（该矩形区域内无其他信号来源，基站工作正常）．若在该矩形区域内随机地选一地点，则该地点无信号的概率是（　　）

A．1- π 4

B． π 2 -1

C．2- π 2

D． π 4

Answer 1

∵扇形ADE的半径为1，圆心角等于90°
∴扇形ADE的面积为S₁=

1

4

×π×1²=

π

4

同理可得，扇形CBF的在，面积S₂=

π

4

又∵长方形ABCD的面积S=2×1=2
∴在该矩形区域内随机地选一地点，则该地点无信号的概率是
P=

S-(S1+S2)

S

=

2-( π 4 + π 4 )

2

=1-

π

4

故答案为：1-

π

4