题目内容
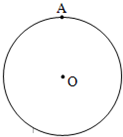
设点A为半径是1的圆O上一定点,在圆周上等可能地任取一点B.
(1)求弦AB的长超过圆内接正三角形边长的概率;
(2)求弦AB的长超过圆半径的概率.
(1)求弦AB的长超过圆内接正三角形边长的概率;
(2)求弦AB的长超过圆半径的概率.

(1)设“弦AB的长超过圆内接正三角形边长”为事件M,
以点A为一顶点,在圆中作一圆内接正三角形ACD,如右图所示,
则要满足题意点B只能落在劣弧CD上,又圆内接正三角形ACD恰好将圆周3等分,
故P(M)=
=
(2)在圆上其他位置任取一点B,圆半径为1,
则B点位置所有情况对应的弧长为圆的周长2π,
其中满足条件AB的长度大于等于半径长度的对应的弧长为
•2π•1,
则AB弦的长度大于等于半径长度的概率P=
=
.
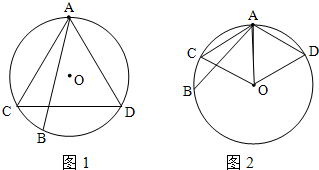
以点A为一顶点,在圆中作一圆内接正三角形ACD,如右图所示,
则要满足题意点B只能落在劣弧CD上,又圆内接正三角形ACD恰好将圆周3等分,
故P(M)=
| 劣弧CD的长 |
| 圆周长 |
| 1 |
| 3 |
(2)在圆上其他位置任取一点B,圆半径为1,
则B点位置所有情况对应的弧长为圆的周长2π,
其中满足条件AB的长度大于等于半径长度的对应的弧长为
| 2 |
| 3 |
则AB弦的长度大于等于半径长度的概率P=
| ||
| 2π•1 |
| 2 |
| 3 |


练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目

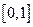 上任取两个数
上任取两个数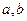 ,方程
,方程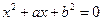 的两根均为实数的概率为 ;
的两根均为实数的概率为 ;