Question

已知正方形ABCD的边长为2，H是边DA的中点．在正方形ABCD内部随机取一点P，则满足|PH|＜

2

的概率为（　　）

A． π 8

B． π 8 + 1 4

C． π 4

D． π 4 + 1 4

Answer 1

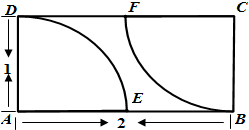
（1）如图所示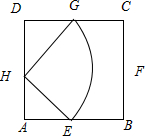，正方形的面积S_{正方形ABCD}=2×2=4．
设“满足|PH|＜

2

的正方形内部的点P的集合”为事件M，
则S（M）=S_△DGH+S_△AEH+S_扇形EGH=2×

1

2

×1×1+

1

2

×

2

×

π

2

×

2

=1+

π

2

，
∴P（M）=

1+ π 2

4

=

π

8

+

1

4

．
故满足|PH|＜

2

的概率为

π

8

+

1

4

．
故选B．