题目内容
已知方程x2+2ax+b2=0是关于x的一元二次方程.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实数根的概率;
(2)若a,b分别是区间[0,3],[0,2]内的随机数,求上述方程有实数根的概率.
(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实数根的概率;
(2)若a,b分别是区间[0,3],[0,2]内的随机数,求上述方程有实数根的概率.
设事件A为“方程x2+2ax+b2=0有实数根”.
当a≥0,b≥0时,方程x2+2ax+b2=0有实数根的充要条件为a≥b.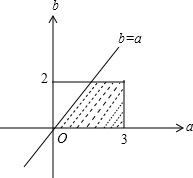
(1)基本事件共12个:(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),
(2,1),(2,2),(3,0),(3,1),(3,2).其中第一个数表示a的取值,第二个数表示b的取值.
事件A中包含9个基本事件.
事件A发生的概率为P(A)=
=
;
(2)试验的全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤2}.
构成事件A的区域为{(a,b)|0≤a≤3,0≤b≤2,a≥b}.
如图,
∴所求的概率P=
=
.
当a≥0,b≥0时,方程x2+2ax+b2=0有实数根的充要条件为a≥b.

(1)基本事件共12个:(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),
(2,1),(2,2),(3,0),(3,1),(3,2).其中第一个数表示a的取值,第二个数表示b的取值.
事件A中包含9个基本事件.
事件A发生的概率为P(A)=
| 9 |
| 12 |
| 3 |
| 4 |
(2)试验的全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤2}.
构成事件A的区域为{(a,b)|0≤a≤3,0≤b≤2,a≥b}.
如图,
∴所求的概率P=
3×2-
| ||
| 3×2 |
| 2 |
| 3 |

练习册系列答案
相关题目