题目内容
(1)袋中共有6个除了颜色外完全相同的球,其中有1个红球,2个白球和3个黑球,从袋中任取两球,求两球颜色为一白一黑的概率.
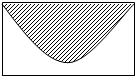
(2)2人相约上午7点到8点之间在某地会面,约定先到的人等候另一人20分钟后可以离开,试求两人能见面的概率.
(2)2人相约上午7点到8点之间在某地会面,约定先到的人等候另一人20分钟后可以离开,试求两人能见面的概率.
(1)根据题意,袋中共有6个球,从中任取2个,有C62=15种不同的取法,
6个球中,有2个白球和3个黑球,则取出的两球为一白一黑的情况有2×3=6种;
则两球颜色为一白一黑的概率P=
=
.
(2)由题意知本题是一个几何概型,设事件A为“两人能会面”,
试验包含的所有事件是Ω={(x,y)|7<x<8,7<y<8},并且事件对应的集合表示的面积是s=1,
满足条件的事件是A={(x,y)|7<x<8,7<y<8,|x-y|<
}
所以事件对应的集合表示的面积是1-2×
×
×
=
,
根据几何概型概率公式得到P=
.
6个球中,有2个白球和3个黑球,则取出的两球为一白一黑的情况有2×3=6种;
则两球颜色为一白一黑的概率P=
| 6 |
| 15 |
| 2 |
| 5 |
(2)由题意知本题是一个几何概型,设事件A为“两人能会面”,
试验包含的所有事件是Ω={(x,y)|7<x<8,7<y<8},并且事件对应的集合表示的面积是s=1,
满足条件的事件是A={(x,y)|7<x<8,7<y<8,|x-y|<
| 20 |
| 60 |
所以事件对应的集合表示的面积是1-2×
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
| 9 |
根据几何概型概率公式得到P=
| 5 |
| 9 |

练习册系列答案
相关题目

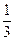 .求游戏者获胜的概率?
.求游戏者获胜的概率?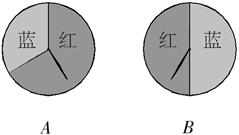
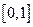 上任取两个数
上任取两个数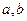 ,方程
,方程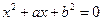 的两根均为实数的概率为 ;
的两根均为实数的概率为 ;