题目内容
14.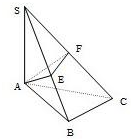 如图,已知SA⊥平面ABC,AB⊥BC,过点A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F
如图,已知SA⊥平面ABC,AB⊥BC,过点A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F(1)求证:AE⊥平面SBC;
(2)求证:SC⊥AF;
(3)判断直线BC是否平行于平面AEF,请说明理由.
分析 (1)由已知中过A作SB的垂线,垂足为E,由线面垂直的判定定理可得AE⊥面SBC,
(2)结合(1)的结论,进而AE⊥SC,再由已知中,过E作SC的垂线,垂足为F,由线面垂直的判定定理可得SC⊥面AEF,最后由线面垂直的性质得到AF⊥SC.
(3)设BC∥平面AEF,可得BC∥EF,由EF⊥SC,可证BC⊥SC,可证BC⊥平面SAC,AC?平面SAC,从而证明BC⊥AC,这与AB⊥BC矛盾,从而证明直线BC不平行于平面AEF.
解答  证明:(1)∵AE⊥BC,AE⊥SB,且SB∩BC=B,
证明:(1)∵AE⊥BC,AE⊥SB,且SB∩BC=B,
∴AE⊥面SBC.
(2)由(1)得AE⊥面SBC,
∵SC?面SBC,
故AE⊥SC.
又∵AE⊥SC,EF⊥SC,且AE∩EF=E,
∴SC⊥面AEF,
∵AF?面AEF,
故AF⊥SC.
(3)直线BC不平行于平面AEF,
证明如下(反证法):设BC∥平面AEF,
∵平面SCB∩平面AEF=EF,
∴BC∥EF,
∵EF⊥SC,
∴BC⊥SC,
又∵BC⊥SA,SA∩SC=S,
∴BC⊥平面SAC,AC?平面SAC,
∴BC⊥AC,
∴△ABC中,与AB⊥BC矛盾.
故直线BC不平行于平面AEF.
点评 本题考查的知识点是直线与平面垂直的判定定理和性质定理,空间中直线与直线之间的位置关系,熟练掌握直线与直线垂直及直线与平面垂直之间的辩证关系及转化方法,是解答本题的关键.

练习册系列答案
相关题目
5.已知四边形ABCD为平行四边形,A(-1,2),B(0,0),C(1,7),则点D的坐标是( )
| A. | (-9,9) | B. | (-9,0) | C. | (0,9) | D. | (0,-9) |
2.下列不等式中成立的是( )
| A. | 若a>b,则ac2>bc2 | B. | 若a>b,则a2>b2 | ||
| C. | 若a<b<0,则a2<ab<b2 | D. | 若a<b<0,则$\frac{1}{a}$>$\frac{1}{b}$ |
19.抛物线x2=8y上的一点M到x轴的距离为4,则点M到抛物线焦点的距离是( )
| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
6.通过随机抽样用样本估计总体,下列说法正确的是( )
| A. | 样本的结果就是总体的结果 | |
| B. | 样本容量越大,可能估计就越精确 | |
| C. | 样本的标准差可以近似地反映总体的平均状态 | |
| D. | 样本数据的中位数一定是总体数据中的中位数 |