题目内容
19．抛物线x2=8y上的一点M到x轴的距离为4，则点M到抛物线焦点的距离是（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 12 |
分析 求得抛物线x2=4y的焦点为（0，2），准线方程为y=-2，设M（m，n），则由抛物线的定义可得点M到抛物线焦点的距离．
解答 解：抛物线x2=4y的焦点为（0，2），准线方程为y=-2
设M（m，n），则由抛物线的定义可得，
M到此抛物线的焦点的距离即为M到准线的距离：为2+4=6．
故选：B．
点评 本题考查抛物线的定义、方程和性质，主要考查定义法的运用，以及准线方程的运用，属于基础题．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
9．函数f（x）=ex-ex在[0，2]上的最大值为（ ）
| A． | 0 | B． | 1 | C． | e-2 | D． | e（e-2） |
7．若|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=$\sqrt{2}$，且（$\overrightarrow{a}$-$\overrightarrow{b}$）•$\overrightarrow{a}$=0，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{3}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | π |
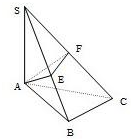如图，已知SA⊥平面ABC，AB⊥BC，过点A作SB的垂线，垂足为E，过E作SC的垂线，垂足为F