题目内容
4.已知:α∈($\frac{π}{4}$,$\frac{3π}{4}$),β∈(0,$\frac{π}{4}$),且cos($\frac{π}{4}$-α)=$\frac{3}{5}$,sin($\frac{5}{4}π$+β)=-$\frac{12}{13}$,则cos(α+β)=$-\frac{33}{65}$.分析 由题意和同角三角函数基本关系可得sin($\frac{π}{4}$-α)和cos($\frac{5}{4}π$+β)的值,由三角函数公式可得cos(α+β)=-cos[($\frac{5}{4}π$+β)-($\frac{π}{4}$-α)]=-cos($\frac{5}{4}π$+β)cos($\frac{π}{4}$-α)-sin($\frac{5}{4}π$+β)sin($\frac{π}{4}$-α),代值计算可得.
解答 解:∵α∈($\frac{π}{4}$,$\frac{3π}{4}$),∴$\frac{π}{4}$-α∈($-\frac{π}{2}$,0),
∵cos($\frac{π}{4}$-α)=$\frac{3}{5}$,∴sin($\frac{π}{4}$-α)=-$\frac{4}{5}$,
同理由β∈(0,$\frac{π}{4}$)和sin($\frac{5}{4}π$+β)=-$\frac{12}{13}$可得cos($\frac{5}{4}π$+β)=-$\frac{5}{13}$,
∴cos(α+β)=-cos[π+(α+β)]=-cos[($\frac{5}{4}π$+β)-($\frac{π}{4}$-α)]
=-cos($\frac{5}{4}π$+β)cos($\frac{π}{4}$-α)-sin($\frac{5}{4}π$+β)sin($\frac{π}{4}$-α)
=$\frac{5}{13}×\frac{3}{5}-(-\frac{12}{13})×(-\frac{4}{5})$=$-\frac{33}{65}$,
故答案为:$-\frac{33}{65}$.
点评 本题考查两角和与差的三角函数公式,涉及同角三角函数的基本关系,属基础题.

 阅读快车系列答案
阅读快车系列答案 我校要对高一学生的数学成绩进行调查,现从中随机抽出若干名学生的数学成绩进行分析,绘制频率分布直方图如图,若低于60分的人数是15,
我校要对高一学生的数学成绩进行调查,现从中随机抽出若干名学生的数学成绩进行分析,绘制频率分布直方图如图,若低于60分的人数是15,(1)试求抽出的学生人数.
(2)试估计高一学生数学成绩的平均值.
| A. | (-4,2) | B. | (-2,0) | C. | (-4,0) | D. | (0,2) |
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4 | D. | 8 |
| A. | 0 | B. | 1 | C. | e-2 | D. | e(e-2) |
| A. | 20$\sqrt{6}$米 | B. | 20$\sqrt{3}$米 | C. | 20$\sqrt{2}$米 | D. | 20米 |
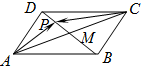 如图,平行四边形ABCD的两条对角线相交于点M,点P是MD中点,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,且∠BAD=60°,则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为( )
如图,平行四边形ABCD的两条对角线相交于点M,点P是MD中点,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,且∠BAD=60°,则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为( )| A. | -$\frac{5}{16}$ | B. | -$\frac{15}{16}$ | C. | -$\frac{25}{16}$ | D. | -$\frac{27}{16}$ |
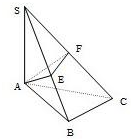 如图,已知SA⊥平面ABC,AB⊥BC,过点A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F
如图,已知SA⊥平面ABC,AB⊥BC,过点A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F