题目内容
3.若数列{an}满足a1=2,an=1-$\frac{1}{{a}_{n-1}}$,则a2013=-1.分析 由a1=2,an=1-$\frac{1}{{a}_{n-1}}$可得数列{an}的值呈周期出现,周期为3;从而求得.
解答 解:∵a1=2,an=1-$\frac{1}{{a}_{n-1}}$,
∴a2=1-$\frac{1}{{a}_{1}}$=$\frac{1}{2}$,
a3=1-$\frac{1}{{a}_{2}}$=-1,
a4=1-$\frac{1}{{a}_{3}}$=2,
a5=1-$\frac{1}{{a}_{4}}$=$\frac{1}{2}$,
…
∴数列{an}的值呈周期出现,周期为3;
且2013=2010+3,
∴a2013=a3=-1.
故答案为:-1.
点评 本题考查了数列的递推公式的应用及周期性的应用,属于基础题.

练习册系列答案
相关题目
13.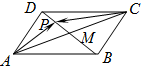 如图,平行四边形ABCD的两条对角线相交于点M,点P是MD中点,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,且∠BAD=60°,则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为( )
如图,平行四边形ABCD的两条对角线相交于点M,点P是MD中点,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,且∠BAD=60°,则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为( )
 如图,平行四边形ABCD的两条对角线相交于点M,点P是MD中点,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,且∠BAD=60°,则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为( )
如图,平行四边形ABCD的两条对角线相交于点M,点P是MD中点,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,且∠BAD=60°,则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为( )| A. | -$\frac{5}{16}$ | B. | -$\frac{15}{16}$ | C. | -$\frac{25}{16}$ | D. | -$\frac{27}{16}$ |
18.已知等差数列{an}的通项公式an=2-2n,则它的公差为( )
| A. | -2 | B. | 3 | C. | 2 | D. | -3 |
12.设f(x)是定义在R上的偶函数,且f(2+x)=f(2-x),当x∈[-2,0]时,f(x)=($\frac{\sqrt{2}}{2}$)x-1,若函数g(x)=f(x)-loga(x+2)(a>0)且a≠0在区间(-2,6)内恰有4个零点,则实数a的取值范围是( )
| A. | ($\frac{1}{4}$,1) | B. | (1,4) | C. | (8,+∞) | D. | (1,8) |
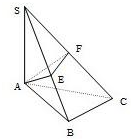 如图,已知SA⊥平面ABC,AB⊥BC,过点A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F
如图,已知SA⊥平面ABC,AB⊥BC,过点A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F 如图所示,是一个底面直径为20cm的装有一部分水的圆柱形玻璃杯,一个底面直径为12cm,高为8cm的圆锥形铅锤完全浸没在水中.
如图所示,是一个底面直径为20cm的装有一部分水的圆柱形玻璃杯,一个底面直径为12cm,高为8cm的圆锥形铅锤完全浸没在水中.