题目内容
2.下列不等式中成立的是( )| A. | 若a>b,则ac2>bc2 | B. | 若a>b,则a2>b2 | ||
| C. | 若a<b<0,则a2<ab<b2 | D. | 若a<b<0,则$\frac{1}{a}$>$\frac{1}{b}$ |
分析 运用列举法和不等式的性质,逐一进行判断,即可得到结论.
解答 解:对于A,若a>b,c=0,则ac2=bc2,故A不成立;
对于B,若a>b,比如a=2,b=-2,则a2=b2,故B不成立;
对于C,若a<b<0,比如a=-3,b=-2,则a2>ab,故C不成立;
对于D,若a<b<0,则a-b<0,ab>0,即有$\frac{a-b}{ab}$<0,即$\frac{1}{b}$<$\frac{1}{a}$,则$\frac{1}{a}$>$\frac{1}{b}$,故D成立.
故选:D.
点评 本题考查不等式的性质和运用,注意运用列举法和不等式的性质是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
12.已知x>0,y>0,且$\frac{2}{x}$+$\frac{1}{y}$=1,若x+2y>m2+2m恒成立,则实数m的取值范围是( )
| A. | (-4,2) | B. | (-2,0) | C. | (-4,0) | D. | (0,2) |
13.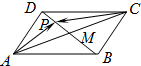 如图,平行四边形ABCD的两条对角线相交于点M,点P是MD中点,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,且∠BAD=60°,则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为( )
如图,平行四边形ABCD的两条对角线相交于点M,点P是MD中点,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,且∠BAD=60°,则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为( )
 如图,平行四边形ABCD的两条对角线相交于点M,点P是MD中点,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,且∠BAD=60°,则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为( )
如图,平行四边形ABCD的两条对角线相交于点M,点P是MD中点,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,且∠BAD=60°,则$\overrightarrow{AP}$$•\overrightarrow{CP}$的值为( )| A. | -$\frac{5}{16}$ | B. | -$\frac{15}{16}$ | C. | -$\frac{25}{16}$ | D. | -$\frac{27}{16}$ |
7.若|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{2}$,且($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=0,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
12.设f(x)是定义在R上的偶函数,且f(2+x)=f(2-x),当x∈[-2,0]时,f(x)=($\frac{\sqrt{2}}{2}$)x-1,若函数g(x)=f(x)-loga(x+2)(a>0)且a≠0在区间(-2,6)内恰有4个零点,则实数a的取值范围是( )
| A. | ($\frac{1}{4}$,1) | B. | (1,4) | C. | (8,+∞) | D. | (1,8) |
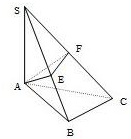 如图,已知SA⊥平面ABC,AB⊥BC,过点A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F
如图,已知SA⊥平面ABC,AB⊥BC,过点A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F