题目内容
4.若不等式|3x+2|≥|2x+a|对x∈R恒成立,求a范围.分析 问题转化为5x2+4(3-a)x+(4-a2)≥0对x∈R恒成立,结合二次函数的性质得到不等式,解出即可.
解答 解:|3x+2|≥|2x+a|
?9x2+12x+4≥4x2+4ax+a2
?5x2+4(3-a)x+(4-a2)≥0
要使x∈R恒成立,即使判别式△≤0.
也即[4(3-a)]2-20(4-a2)≤0.
?9a2-24a+16≤0
?(3a-4)2≤0
?a=$\frac{4}{3}$.
点评 本题考查了绝对值不等式的解法,考查二次函数的性质,是一道中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
12.设f(x)是定义在R上的偶函数,且f(2+x)=f(2-x),当x∈[-2,0]时,f(x)=($\frac{\sqrt{2}}{2}$)x-1,若函数g(x)=f(x)-loga(x+2)(a>0)且a≠0在区间(-2,6)内恰有4个零点,则实数a的取值范围是( )
| A. | ($\frac{1}{4}$,1) | B. | (1,4) | C. | (8,+∞) | D. | (1,8) |
19.从3名女同学和2名男同学中选1人主持本班的某次主题班会,则不同的选法为( )
| A. | 3 | B. | 5 | C. | 6 | D. | 10 |
16.下列各组表示同一函数的是( )
| A. | y=$\sqrt{{x}^{2}}$与y=($\sqrt{x}$)2 | B. | y=lgx2与y=2lgx | ||
| C. | y=1+$\frac{1}{x}$与y=1+$\frac{1}{t}$ | D. | y=x2-1(x∈R)与y=x2-1(x∈N) |
14.设f(x)=${∫}_{-x}^{x}$cos2tdt,则f(f($\frac{π}{4}$))=
| A. | 1 | B. | sin 1 | C. | sin 2 | D. | 2sin 4 |
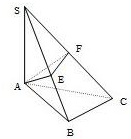 如图,已知SA⊥平面ABC,AB⊥BC,过点A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F
如图,已知SA⊥平面ABC,AB⊥BC,过点A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F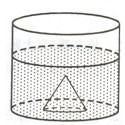 如图所示,是一个底面直径为20cm的装有一部分水的圆柱形玻璃杯,一个底面直径为12cm,高为8cm的圆锥形铅锤完全浸没在水中.
如图所示,是一个底面直径为20cm的装有一部分水的圆柱形玻璃杯,一个底面直径为12cm,高为8cm的圆锥形铅锤完全浸没在水中.